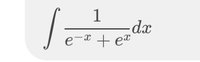Integrate 1/[e^x + e^(-x)]

[MERRVYN]

How to integrate 1/[e^x + e^(-x)]

 

[Deleted member 4993]

How to integrate 1/[e^x + e^(-x)]

Hint: Use substitution:

u = e^x \(\displaystyle \ \to \ \) dx = du/u

Please show us what you have tried and exactly where you are stuck.

Please follow the rules of posting in this forum, as enunciated at:

https://www.freemathhelp.com/forum/threads/read-before-posting.109846/#post-486520​

Please share your work/thoughts about this problem.

 

[HallsofIvy]

My first thought: Multiply numerator and denominator of \(\displaystyle \frac{dx}{e^x+ e^{-x}}\) by \(\displaystyle e^x\) to get \(\displaystyle \frac{e^x dx}{e^{2x}+ 1}\).

Then let \(\displaystyle u= e^x\). \(\displaystyle du= e^x dx\) so the integrand becomes \(\displaystyle \frac{udu}{u^2+ 1}\). Now let \(\displaystyle v= u^2+ 1\) so that \(\displaystyle dv= 2udu\) and the integrand becomes \(\displaystyle \frac{1}{2}\frac{dv}{v}\).

 

[pka]

How to integrate 1/[e^x + e^(-x)]

HINT: think \(\arctan(u)\).

 

[joshuaa]

if you wanna be fancy, do it like this

[MATH]\int \frac{1}{e^x + e^{-x}} \ dx = \frac{1}{2}\int \sech x \ dx[/MATH]

 

[Steven G]

if you wanna be fancy, do it like this

[MATH]\int \frac{1}{e^x + e^{-x}} \ dx = \frac{1}{2}\int \sech x \ dx[/MATH]

It is not being fancy, it IS the way to solve this (assuming that you learned about hyperbolic functions).