Can someone please explain this problem to me: I have to use integrals to find volumes with known cross sections but i just don't understand. Thanks!
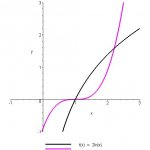
Consider a solid bounded by y=2ln(x) and y=0.9((x-1)^3) in the first quadrant. If cross sections taken perpendicular to the x-axis are isosceles right triangles with the hypotenuse in the base, find the volume of this solid.
Consider a solid bounded by y=2ln(x) and y=0.9((x-1)^3) in the first quadrant. If cross sections taken perpendicular to the x-axis are isosceles right triangles with the hypotenuse in the base, find the volume of this solid.