Integrals + Area under the graph

[1141]

A little help, please?

The question is: Find the area of the region shaded in each of the following diagrams.

I don't know how I would go about doing the attached graphs. How do I find the other x value?

 

[arthur ohlsten]

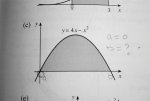
y=4-x^2
let y=0
x^2=4
x=+/- 2
the value of b is 2,0

area= int. [4-x^2] dx from 0 to 2

===============================================================
y=4x-x^2 factor out x
y=x[4-x^2]
let y=0
0=x[4-x^2
x=0 or 4-x^2=0
4-x^2=0
x=+/-2

a=0
b=2

Arthur

 

[1141]

Ah, so simple! I wasn't paying attention properly! Thanks.

I got the right answer for a.), but for b.) I only get half of what the correct answer should be. I get 16/3 when the answer should be 32/3.
Can you tell me where I went wrong.

?[sup:3bghdy9v]a[/sup:3bghdy9v][sub:3bghdy9v]b[/sub:3bghdy9v] f(x) dx

= ?[sup:3bghdy9v]2[/sup:3bghdy9v][sub:3bghdy9v]0[/sub:3bghdy9v] 4x - x[sup:3bghdy9v]2[/sup:3bghdy9v] dx

= [2x[sup:3bghdy9v]2[/sup:3bghdy9v] - 1/3x[sup:3bghdy9v]3[/sup:3bghdy9v]][sup:3bghdy9v]2[/sup:3bghdy9v][sub:3bghdy9v]0[/sub:3bghdy9v]

? I(a) = 2(0)[sup:3bghdy9v]2[/sup:3bghdy9v] - 1/3(0)[sup:3bghdy9v]3[/sup:3bghdy9v]
= 0

? I(b) = 2(2)[sup:3bghdy9v]2[/sup:3bghdy9v] - 1/3(2)[sup:3bghdy9v]3[/sup:3bghdy9v]
= 16/3

? I(b) - I(a)
= 16/3 -0
=16/3

 

[Deleted member 4993]

Ah, so simple! I wasn't paying attention properly! Thanks.

I got the right answer for a.), but for b.) I only get half of what the correct answer should be. I get 16/3 when the answer should be 32/3.
Can you tell me where I went wrong.

?[sup:3jwrcj3n]a[/sup:3jwrcj3n][sub:3jwrcj3n]b[/sub:3jwrcj3n] f(x) dx

= ?[sup:3jwrcj3n]2[/sup:3jwrcj3n][sub:3jwrcj3n]0[/sub:3jwrcj3n] 4x - x[sup:3jwrcj3n]2[/sup:3jwrcj3n] dx

= [2x[sup:3jwrcj3n]2[/sup:3jwrcj3n] - 1/3x[sup:3jwrcj3n]3[/sup:3jwrcj3n]][sup:3jwrcj3n]2[/sup:3jwrcj3n][sub:3jwrcj3n]0[/sub:3jwrcj3n]

? I(a) = 2(0)[sup:3jwrcj3n]2[/sup:3jwrcj3n] - 1/3(0)[sup:3jwrcj3n]3[/sup:3jwrcj3n]
= 0

? I(b) = 2(2)[sup:3jwrcj3n]2[/sup:3jwrcj3n] - 1/3(2)[sup:3jwrcj3n]3[/sup:3jwrcj3n]
= 16/3

? I(b) - I(a)
= 16/3 -0
=16/3

Your limits are incorrect

Recalculate value of 'b'.

 

[1141]

Okay, I got the right answer now. I recalculated "b" and it was equal to 4, not 2.

I have the same problem with two other questions - I get either half or doubled of what I'm supposed to get.

Attached are the two questions. The answer for e.) is supposed to be 500, but I get 250:
Here is my working:

?[sub:2a2ku9zi]a[/sub:2a2ku9zi][sup:2a2ku9zi]b[/sup:2a2ku9zi] f(x) dx

= ?[sub:2a2ku9zi]0[/sub:2a2ku9zi][sup:2a2ku9zi]5[/sup:2a2ku9zi] 6x[sup:2a2ku9zi]2[/sup:2a2ku9zi] dx

= [6( 1/3x[sup:2a2ku9zi]3[/sup:2a2ku9zi])][sub:2a2ku9zi]0[/sub:2a2ku9zi][sup:2a2ku9zi]5[/sup:2a2ku9zi]

=[2x[sup:2a2ku9zi]3[/sup:2a2ku9zi]][sub:2a2ku9zi]0[/sub:2a2ku9zi][sup:2a2ku9zi]5[/sup:2a2ku9zi]

? I(a) = 2(0)[sup:2a2ku9zi]3[/sup:2a2ku9zi]
= 0

? I(b) = 2(5)[sup:2a2ku9zi]3[/sup:2a2ku9zi]
= 250

? I(b) - I(a)
= 250 - 0
= 250

You have calculated the area "under" the curve - the question was about the area "over" the curve. so the answer should be

Area = 5 * 150 - 250 = 500

For question f.) the answer is supposed to be 16/3 but I get 32/3.
My working out:

?[sub:2a2ku9zi]a[/sub:2a2ku9zi][sup:2a2ku9zi]b[/sup:2a2ku9zi] f(x) dx

= ?[sub:2a2ku9zi]-1[/sub:2a2ku9zi][sup:2a2ku9zi]1[/sup:2a2ku9zi] 3x[sup:2a2ku9zi]8[/sup:2a2ku9zi] + 5 dx

= [3( 1/9x[sup:2a2ku9zi]9[/sup:2a2ku9zi]) + 5( 1/1x)][sub:2a2ku9zi]-1[/sub:2a2ku9zi][sup:2a2ku9zi]1[/sup:2a2ku9zi]

= [1/3x[sup:2a2ku9zi]9[/sup:2a2ku9zi] + 5x][sub:2a2ku9zi]-1[/sub:2a2ku9zi][sup:2a2ku9zi]1[/sup:2a2ku9zi]

? I(a) = 1/3(-1)[sup:2a2ku9zi]9[/sup:2a2ku9zi] + 5(-1)
= -16/3

? I(b) = 1/3(1)[sup:2a2ku9zi]9[/sup:2a2ku9zi] + 5(1)
= 16/3

? I(b) - I(a)
= 16/3 - (-16/3)
= 16/3 + 16/3
= 32/3



Can you tell me where I'm going wrong in these questions too?

 

[1141]

Okay, understand about the area "over" the curve, but why do I mulitply by 5? And what about the next question?

 

[pitoten]

When you take the integral of the curves in these situations, it is always equal to the area between a and b and between the curve and the x axis. That's always how it works in these situations. But they are not asking for that in your problems. But fortunately, you can use the area under the curves to figure out the answers anyway...

For e, the answer you are looking for is (the area of the square with sides 150 and 5) - (the area between the curve and the x axis).

Similar logic applies to f.

 

[1141]

For e, the answer you are looking for is (the area of the square with sides 150 and 5) - (the area between the curve and the x axis).

Okay, I completely understand now! I don't know why I didn't see that before.
Thank you so much! I did each question again and I got right, first try.