Integral rate of flow

[ffuh205]

The differential equation dy/dx = 2x^3 + 2 cos(x/2) - (1.2) ^x gives the rate of flow of water in/out of a reservoir in gallons per minute.

a) Find the general solution to the differential equation and its particular solution through the point (1, 2). Interpret the meaning for the particular solution.

b) For this particular solution list the points of max, Min, and points of Inflection, domain, Range, Intervals for Continuity, and Differentiability.


For A, this is what I got. [(5/6) ^-x]/ [ln (5/6)] + 4sin(x/2) + (x^4)/2 + C
2 = [(5/6) ^-1]/ [ln (5/6)] + 4sin (1/2) + (1^4)/2 + C; 2 = -164.544 + 1.918 + .5 + C; C = 162.126
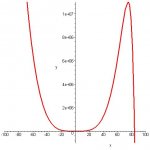
[(5/6) ^-x]/ [ln (5/6)] + 4sin(x/2) + (x^4)/2 + 162.13

I think I am doing this correctly but when I look at b, it becomes clear that the function and the integral will always be positive based on my work. That being the case, there would be no min max or inflection point. Also, I am not sure if it wants me to find the questions in b for the original function or the integral.

 

[tkhunny]

You should make up your mind on that exponent on 1.2. Is it 'x' or '-x'. Positive works better.

 

[BigGlenntheHeavy]

\(\displaystyle \frac{dy}{dx} \ = \ 2x^3+2cos(x/2)-1.2^x \ \ \implies \ y(x) \ = \ \frac{x^4}{2}+4sin(x/2)-\frac{(6/5)^x}{ln(6/5)}+C\)

\(\displaystyle y(1) \ = \ 2 \ = \ \frac{1}{2}+4sin(1/2)-\frac{6/5}{ln(6/5)}+C \ \implies \ C \ = \ 6.164\)

\(\displaystyle a) \ Hence, \ y(x) \ = \ \frac{x^4}{2}+4sin(x/2)-\frac{(6/5)^x}{ln(6/5)}+6.164\)

\(\displaystyle b) \ Max. \ (74.8,11061116) \ Min. \ (-.7886,.0704), \ Pts. \ of \ inflection: \ (-.1355,.5424),(.224,.9),\)

\(\displaystyle and \ (65,81133570).\)

\(\displaystyle Domain \ (-\infty,\infty), \ Range \ (-\infty,\infty), \ Continuous \ and \ differentiable \ throughout.\)

\(\displaystyle Note; \ One \ solution \ (84,0).\)

\(\displaystyle See \ graph.\)

[attachment=0:2j6wek7b]vwx.jpg[/attachment:2j6wek7b]