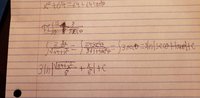Integral of volume over an interval

[Kcashew]

Good evening everyone,

I was wondering if I could get some help with this problem.
My stratchwork was done on the lined paper.

From what I can gather, this problem is asking me to solve the the integral of pi(y^2).

I have tried using trigonometric substitution for y, but I have gotten stuck.

Am I going about this the right way? If not, how should I proceed?

 

[MarkFL]

Problem:

Consider the region \(R\) between the graph of the function [MATH]f(x)=\frac{3}{\sqrt{64+x^2}}[/MATH] and the \(x\)-axis over the interval \([0,15]\).

(a) Find the volume of the solid generated when \(R\) is revolved about the \(x\)-axis.

I would use the disk method, where:

[MATH]dV=\pi\left(\frac{3}{\sqrt{64+x^2}}\right)^2\,dx[/MATH]
Hence:

[MATH]V=9\pi\int_{0}^{15}\frac{1}{x^2+8^2}\,dx[/MATH]
Let:

[MATH]x=8\tan(\theta)\implies dx=8\sec^2(\theta)\,d\theta[/MATH]
[MATH]V=\frac{9\pi}{8}\int_{0}^{\arctan\left(\frac{15}{8}\right)}\frac{\sec^2(\theta)}{\tan^2(\theta)+1}\,d\theta=\frac{9\pi}{8}\int_{0}^{\arctan\left(\frac{15}{8}\right)}\,d\theta[/MATH]
Can you proceed?

 

[Kcashew]

I might be, but I do not understand why arctan(15/8) replaced 15.

Aside from that, I believe the answer would be (9pi * arctan(15/8))/8

 

[MarkFL]

I made the substitution:

[MATH]x=8\tan(\theta)[/MATH]
And this implies:

[MATH]\theta=\arctan\left(\frac{x}{8}\right)[/MATH]
Changing the limits of integration uses the above \(\theta(x)\).

[MATH]\theta(0)=\arctan\left(\frac{0}{8}\right)=0[/MATH]
[MATH]\theta(15)=\arctan\left(\frac{15}{8}\right)[/MATH]
And so I agree that:

[MATH]V=\frac{9\pi}{8}\arctan\left(\frac{15}{8}\right)[/MATH]

 

[Kcashew]

Thank you very much for clarifying that.

Could this be expressed in terms of x, or is that unnecessary considering that θ is no longer a part of the equation?

 

[MarkFL]

When you're dealing with a definite integral, once you make a substitution, and change the integrand, differential and limits to be in terms of the new variable, you need not concern yourself anymore with the old variable at all. In a definite integral, the variable of integration is considered a "dummy variable" because it gets integrated out.

 

[Steven G]

Alternatively when you solve the integral in terms of θ you can substitute back to x's and then use the original limits.