shahar
Full Member
- Joined
- Jul 19, 2018
- Messages
- 519
In the end of the article:
 www.lbscience.org
Escher said:
www.lbscience.org
Escher said:
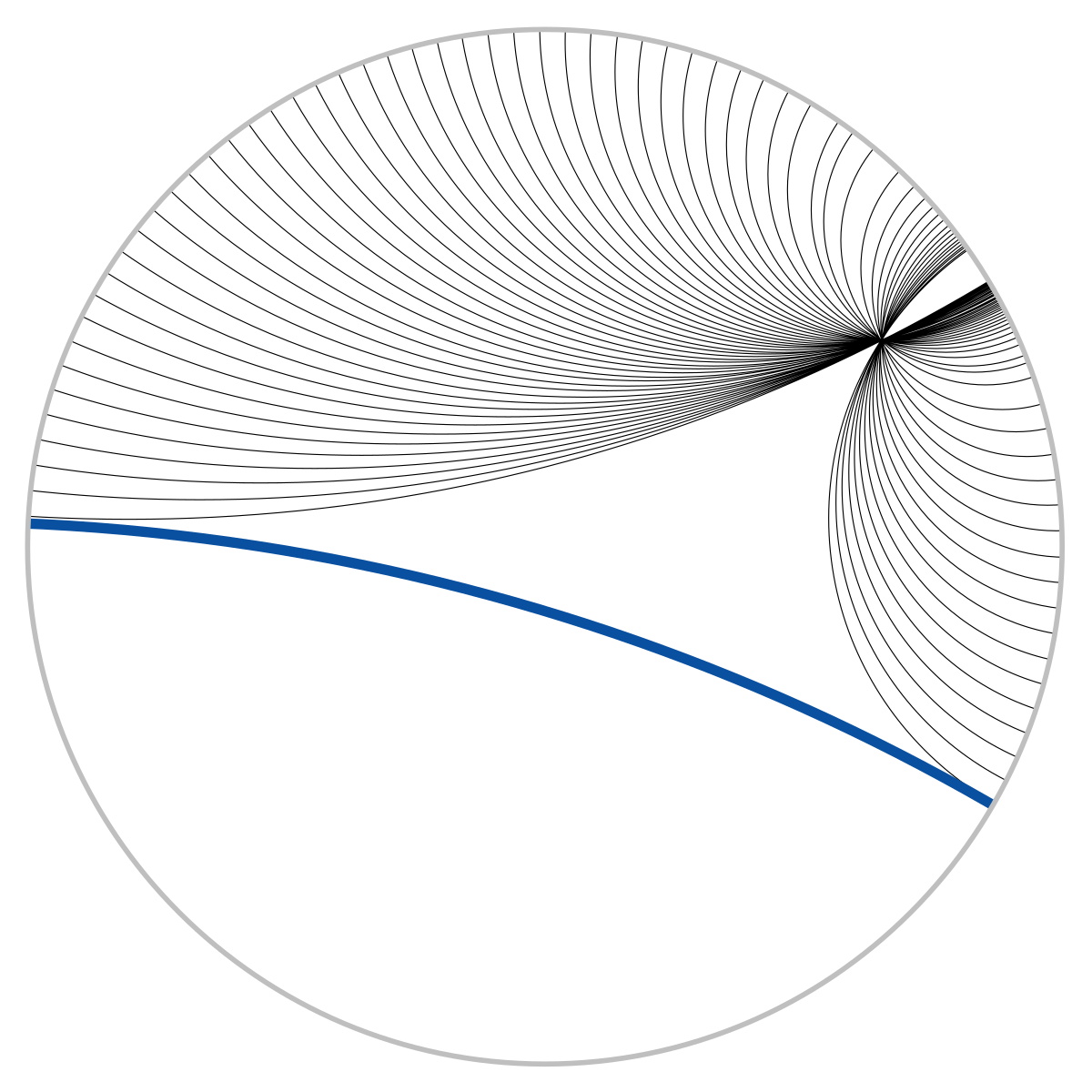
As all these strings of fish shoot up like rockets from infinitely far away, perpendicularly from the boundary, and fall back again whence they came, not one single component ever reaches the edge.
What the meaning of the expression "from infinitely far away"?

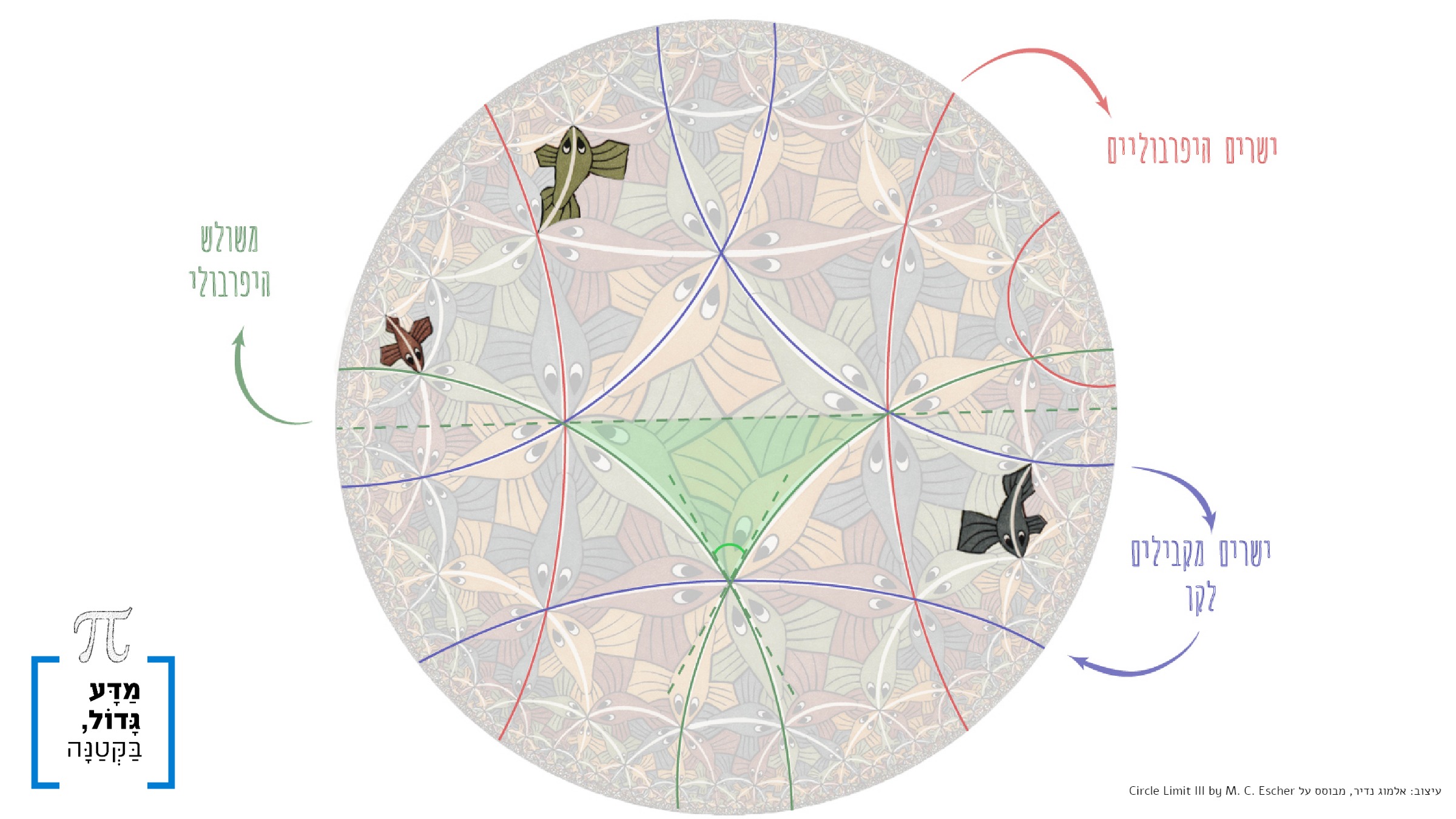
לאן שוחים הדגים של אֶשֶׁר? - מדע גדול, בקטנה
הגאומטריה המוכרת לנו מבית הספר היא הגאומטריה האוקלידית. היא מבוססת על חמש אקסיומות בלבד, שהונחו בתקופת אוקלידס, בסביבות 300 לפני הספירה. אקסיומות הן הנחות יסוד, שמהן נגזרות שלל מסקנות לגבי משולשים, מעגלים וכולי. פרט טריוויה מעניין הוא שהספר ”יסודות” של אוקלידס היה הספר העיקרי ללימוד גאומטריה עד...
 www.lbscience.org
www.lbscience.org
As all these strings of fish shoot up like rockets from infinitely far away, perpendicularly from the boundary, and fall back again whence they came, not one single component ever reaches the edge.
What the meaning of the expression "from infinitely far away"?