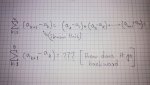Induction...stuck at the middle

[mna_1]

please see the attachment. Thanks in advance....

 

[Harry_the_cat]

Why do you need to put n=0?

Can you post the original question, then we can help?

 

[mna_1]

Hi .. you could see the actual question in attachment. For the first part of induction you gotta for both sides n=1. as you can see right on the middle 1-1=0.:shock:

 

[Ishuda]

Hi .. you could see the actual question in attachment. For the first part of induction you gotta for both sides n=1. as you can see right on the middle 1-1=0.:shock:

When I have run into a situation like this, a smaller value on top indicates the sum is zero, i.e.
if j>0 then
\(\displaystyle \Sigma_{k=m}^{k=m-j}\,\,\, something\, =\, 0\)
This would be correct for n=1 in your problem
\(\displaystyle \Sigma_{k=1}^{k=1}\,\, a_kb_k\, = a_1\, b_1\, =\, a_1\, \Sigma_{k=1}^{k=1}\,\, b_k\, -\, \Sigma_{k=1}^{k=0}\,\, something\, =\, \, a_1\, \Sigma_{k=1}^{k=1}\,\, b_k\, -\, 0\, = a_1\, b_1\)

If you feel uncomfortable with this as a first step in the induction process, you could start the induction process at n=2 and then say something like 'for n=1, it is also true if we interpret the resulting sum from 1 to 0 as zero'.

 

[stapel]

Hi .. you could see the actual question in attachment.

The attachment in your original post appears to show part of your working for "the actual question". If you included "the actual question" in that image, it is not displaying on our end. Sorry.

For the first part of induction you gotta for both sides n=1. as you can see right on the middle 1-1=0.

In your new attachment, at least some of "the actual question" is cut off. In particular, there is nothing about "induction" in either attachment. I will guess that "the actual question" was something along the lines of the following:

. . .\(\displaystyle \mbox{Use induction to prove the following:}\)

. . . . .\(\displaystyle \mbox{For all numbers }\, n\, \in\, \mathbb{N}\, \setminus \, \{0\},\, \mbox{the following equality holds:}\)

. . . . . . .\(\displaystyle \displaystyle \sum_{k = 1}^{n}\, a_k\, b_k\, =\, a_n\, \sum_{k = 1}^{n}\, b_k\, -\, \sum_{k = 1}^{n - 1}\, \left(a_{k + 1}\, -\, a_k\right)\, \sum_{j = 1}^{k}\, b_j\)

Did I guess the exercise right? Is there any additional information we should know regarding the terms a_k and b_k of the various sums?

When you reply, please include a clear listing of your thoughts and efforts so far, so we can see what's going on. Thank you!

 

[mna_1]

You are 100% right. the question matches as it is in my exercise paper (and there is no additional information). i didn't upload "the actual question" because it is in german. apologize for that

 

[mna_1]

When I have run into a situation like this, a smaller value on top indicates the sum is zero, i.e.
if j>0 then
\(\displaystyle \Sigma_{k=m}^{k=m-j}\,\,\, something\, =\, 0\)
This would be correct for n=1 in your problem
\(\displaystyle \Sigma_{k=1}^{k=1}\,\, a_kb_k\, = a_1\, b_1\, =\, a_1\, \Sigma_{k=1}^{k=1}\,\, b_k\, -\, \Sigma_{k=1}^{k=0}\,\, something\, =\, \, a_1\, \Sigma_{k=1}^{k=1}\,\, b_k\, -\, 0\, = a_1\, b_1\)

If you feel uncomfortable with this as a first step in the induction process, you could start the induction process at n=2 and then say something like 'for n=1, it is also true if we interpret the resulting sum from 1 to 0 as zero'.

thnx for the help