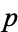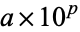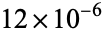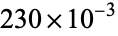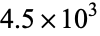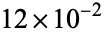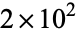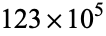Indicies: My solution is 63 x 10^-4 The textbook solution is 6.3 x 10^-3

V

Ventus

New member
Joined
May 31, 2019
Messages
6
Just to start of with I didn't know where to put my issue but here it is,
I am currently focusing on indices at school and I realised that sometimes when the problem asks to put the following number in a scientific notation they write it a bit differently than how I did it. Heres one for example
0.0063. Write this is scientific notation
My solution is 63 x 10-4
The textbook solution is 6.3 x 10-3
I noticed this little difference is repeatedly happening and my answers are always differentiating from the textbook. Is my solution wrong?
Thank you for whoever answers the question
 
Last edited by a moderator:
Have you been taught how to normalize scientific notation, so that the multiplier is always between 1 and 10? That seems to be the step you're missing.

In your example, in order to reduce 63 to the right range, you have to divide it by 10; to compensate for that, you multiply 10-4 by 10, giving 10-3.

Or you can go directly to this form, by counting only three places from the decimal point to past the 6 in 0.0063. Don't count all the way to the end. See here.
 
Another common form, sometimes called "engineering notation" would be \(\displaystyle 0.64\times 10^{-5}\) which has the first non-zero digit immediately after the decimal point. "Scientific notation", by definition, always has exactly one non-zero digit before the decimal point.
 
HallsofIvy said:
Another common form, sometimes called "engineering notation" [...] has the first non-zero digit immediately after the decimal point.
Click to expand...

Hrm... that's curious, because I learned that "engineering notation" is what it's called when you always use a multiple of three for the exponent. For instance, valid engineering notation would be \(123 \times 10^{-3}\) or \(267.85 \times 10^{9}\).
 
ksdhart2 said:
Hrm... that's curious, because I learned that "engineering notation" is what it's called when you always use a multiple of three for the exponent. For instance, valid engineering notation would be \(123 \times 10^{-3}\) or \(267.85 \times 10^{9}\).
Click to expand...
I agree.

From - http://mathworld.wolfram.com/EngineeringNotation.html :

"Engineering notation is a version of scientific notation in which the exponent
p
in expressions of the form
a×10^p
is chosen to always be divisible by 3. Numbers of forms such as
12×10^(-6)
,
230×10^(-3)
, 340, and
4.5×10^3
therefore correspond to engineering notation, while numbers such as
12×10^(-2)
,
2×10^2
, and
123×10^5
do not. 16 of the 20 SI prefixes (excluding centi-, deci-, deka-, and hecto-) correspond to engineering notation."
 
Last edited by a moderator:
mlynn678 said:
Hello,
I am struggling with index laws.
Click to expand...
Please start a new thread with a "problem" (exact problem statement) and your "attempts" to solve the said problem.

Please refer to the guidelines of postingin this forum at:

READ BEFORE POSTING

Welcome to FreeMathHelp.com! Please take the time to read the following before you make your first post. It will help you to get your math questions answered promptly and in the most helpful manner. A summary is available here, but please read the complete guidelines below at your earliest...
www.freemathhelp.com
 
You must log in or register to reply here.
Top