Increasing or Decreasing Trig Function

[harpazo]

State if the function y = sin x is increasing or decreasing in the given interval.

-pi/2 < x < pi/2

Is graphing the best approach?

Can the given interval be expressed as
[-pi/2, pi/2]?

 

[MarkFL]

Since the inequality is strict, you'd want an open interval. Without the calculus, a graph would be a good alternate. Or visualizing a point moving along the unit circle in a counter-clockwise direction from (0,-1) to (0,1) and what is happening to the \(y\)-coordinate of the point.

 

[pka]

Unless this is for a calculus course the answer is yes.
But there is one small correction. \(-\frac{\pi}{2}<x<\frac{\pi}{2}\) is \(\left(\frac{-\pi}{2},\frac{\pi}{2}\right)\)

 

[harpazo]

Since the inequality is strict, you'd want an open interval. Without the calculus, a graph would be a good alternate. Or visualizing a point moving along the unit circle in a counter-clockwise direction from (0,-1) to (0,1) and what is happening to the \(y\)-coordinate of the point.

Calculus 1 shows a better, more precise and efficient graph. How is y = sin x placed on the xy-plane via Calculus 1 techniques? What happens to the y-coordinate as a point moves from (0, -1) to (0, 1) on the unit circle?

 

[harpazo]

Unless this is for a calculus course the answer is yes.
But there is one small correction. \(-\frac{\pi}{2}<x<\frac{\pi}{2}\) is \(\left(\frac{-\pi}{2},\frac{\pi}{2}\right)\)

Yes, I forgot that we use parentheses in terms of the symbols less than or greater than when expressing in interval notation.

 

[MarkFL]

What happens to the y-coordinate as a point moves from (0, -1) to (0, 1) on the unit circle?

Visualize it, and tell me what you see...

 

[harpazo]

Visualize it, and tell me what you see...

What about using calculus to get a better picture? We can look at the slope (the derivative) of the graph. I have not studied derivative IN FULL but I do recall that the
derivative of sin x is cos x.

I also know that cos x is positive from -pi/2 to < pi/2. So, the slope of sin x is positive, it is increases in that interval. Yes?

I say at –pi/2 and pi/2, cos x = 0. I conclude that sin x is not increasing or decreasing. The slope is zero. Yes?

 

[MarkFL]

Visualize it, and tell me what you see...

Move the slider from left to right...as you do watch the point and the horizontal dashed line through the point. As the angle \(a\) increases from [MATH]-\frac{\pi}{2}[/MATH] to [MATH]\frac{\pi}{2}[/MATH] the point and line move up, that is, increase.

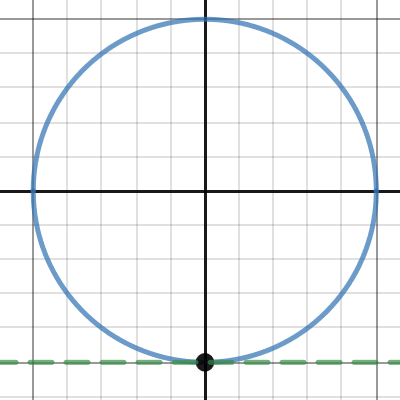
Desmos | Graphing Calculator

www.desmos.com

 

[Otis]

What about using calculus to get a better picture …

At your stage, harpazo, I don't think that's a good idea. I'd use basic trigonometry, first.

The terminal ray of any angle intersects the unit circle at a point. As you trace the unit circle from points (1,0) to (0,1), for example, you're moving through angles in the first quadrant -- that is, between 0 radians (0º) and pi/2 radians (90º).

This is what happens to the x- and y-coordinates of points on the unit circle, as those first-quadrant angles increase: The x-coordinate decreases from 1 to 0, and the y-coordinate increases from 0 to 1. An animated unit-circle tool is available here.

sin(angle) = y-coordinate of point on unit-circle

cos(angle) = x-coordinate of point on unit circle

Therefore, sine increases on the interval (0,pi/2) because the y-coordinates on the unit circle are increasing. Likewise, cosine decreases because the x-coordinates are getting smaller.

Picture angles in the other three quadrants. Visualize tracing the circle in each quadrant. If you can see what's happening to the y-coordinates, then you know what sine is doing.

Memorizing these patterns helped me a lot, when I studied beginning trigonometry.

?

 

[harpazo]

Move the slider from left to right...as you do watch the point and the horizontal dashed line through the point. As the angle \(a\) increases from [MATH]-\frac{\pi}{2}[/MATH] to [MATH]\frac{\pi}{2}[/MATH] the point and line move up, that is, increase.

Desmos | Graphing Calculator

www.desmos.com

I did see that when playing with graph you provided.

 

[harpazo]

At your stage, harpazo, I don't think that's a good idea. I'd use basic trigonometry, first.

The terminal ray of any angle intersects the unit circle at a point. As you trace the unit circle from points (1,0) to (0,1), for example, you're moving through angles in the first quadrant -- that is, between 0 radians (0º) and pi/2 radians (90º).

This is what happens to the x- and y-coordinates of points on the unit circle, as those first-quadrant angles increase: The x-coordinate decreases from 1 to 0, and the y-coordinate increases from 0 to 1. An animated unit-circle tool is available here.

sin(angle) = y-coordinate of point on unit-circle

cos(angle) = x-coordinate of point on unit circle

Therefore, sine increases on the interval (0,pi/2) because the y-coordinates on the unit circle are increasing. Likewise, cosine decreases because the x-coordinates are getting smaller.

Picture angles in the other three quadrants. Visualize tracing the circle in each quadrant. If you can see what's happening to the y-coordinates, then you know what sine is doing.

Memorizing these patterns helped me a lot, when I studied beginning trigonometry.

?

Why did you use parentheses to show the interval (0, pi/2) and not brackets [0, pi/2]?