In triangle ABC, AB=8, BC=6, AC=12; find value of X

[SAASJRBSA]

In triangle ABC, AB=8, BC=6 and AC=12. Each of three segments are drawn through the triangle and intersect at point K which has the length X and each of the three segments drawn throught that triangle, is parallel to a side of the triangle. What is the value of X?

 

[mmm4444bot]

... at point K which has the length X ...

Points do not have length (or width, or depth, or height, or any dimension at all); points have coordinates.

If you are asking about three line segments of equal length X, which all intersect at a single point within the triangle, where each side of the triangle is parallel to one of these line segments, and all three line segments lie entirely within the triangle with each joining two sides of the triangle, then this situation may not be possible.

I could not find a solution using analytical geometry.

Are you able to post an image?

Cheers,

Howard I. Noe

 

[soroban]

Hello, SAASJRBSA!

I haven't solved it yet, but I think I understand the diagram.

In \(\displaystyle \Delta ABC:\; AB=8,\;BC=6,\;AC=12\)

Three line segments are drawn through an interior point \(\displaystyle K.\)

Each segment has length \(\displaystyle x\) and is parallel to a side of the triangle.

What is the value of \(\displaystyle x\) ?

                                    B 
                                    o
                                 *   *
                          P   *       *  T
                           o           o
                  8     *   *       *   *    6
                     *       *   *       *
                S o  *  *  *  o  *  *  *  o R
               *           * K *           * 
            *           *       *           * 
         *           *           *           *
    A o   *   *   o   *   *   *   o   *   *   o C
                 U                 Q
                          12

\(\displaystyle \text{We are given: }\;\begin{Bmatrix} PQ \parallel BC \\ RS \parallel AC \\ TU \parallel AB \end{Bmatrix}\quad\text{ and }\;|PQ| \,=\,|RS| \,=\,|TU| \,=\,x\)

 

[SAASJRBSA]

Yes,
That diagram you drew looks correct! Now, how do you figure out how to solve for X?

 

[Deleted member 4993]

That would be your problem .....

 

[mmm4444bot]

... how do you figure out how ...?

You need to access your own knowledge of geometry, algebra, theorems, perhaps graphing, and all the rest of your skills and intelligence to come up with a strategy.

If your first method fails to get satisfactory results, then try something else.

I tried analytical geometry by imposing an xy-coordinate system with point A at the origin, point C at (12,0), and point B at (43/6,?455/6).

I set the coordinates of point K as (a, b).

I found equations for the three lines through point K, and I used the distance formula to create a system of two equations in a and b, but I was not able to find any solutions for a and b.

I might have made mistakes, but I gave up before reviewing my work.

My gut feeling is that there are theorem(s) in geometry that make this exercise easier. I don't know much about theories in geometry. Do you?

Cheers,

~ Mark

 

[chivox]

I am not sure such a point K exists in the general case, but it may be possible to find such a point for this particular triangle. I have sketched triangle ABC here:

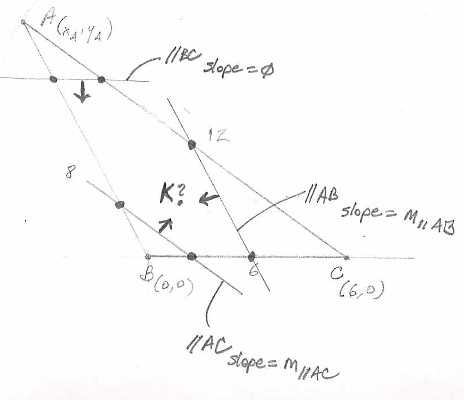
I think you should try to imagine this as an animation, moving each of the parallel line segments toward their intersection (indicated by arrows). I have drawn arrows, but keep in mind that all three segments will also intersect, say, to the right of the segment parallel to AB.

I'm not sure how to solve it yet, but I would probably start by finding the slopes of the lines parallel to AC and AB, solve the system for their intersection. Then, once you have that (there will be an infinite number of points of intersection within triangle ABC), you can use the line parallel to BC (slope = 0 in the diagram) to find the distance, since the y values in all coordinate pairs on that line will be the same for every case of the line.

Looking at the picture, it seems the most likely candidate for a point of intersection where all three segments have the same length will be at a pretty low value of y. If you think about it graphically, the premise of the problem stipulates that all three segments have the same length at some point of intersection. The two non-horizontal segments in my picture will only meet at certain points where they both have the same length. That sounds like you should set their distances equal to each other. If that is indeed how this scenario plays out, I sure hope that horizontal line segment is the same length at one of those points. If not, there can be no solution (using real numbers).

You might also find some interesting theorems about triangles and the lines within them at

http://www.pballew.net/medians.htm

Keep at it. Nice problem, if there's a solution.....

 

[mmm4444bot]

Here's another site with good information about triangles (among other things). I like this site because most of the illustrations are dynamic; you can click-and-drag various components (eg: vertex, midpoint) with the mouse to see how the relationships change. (JAVA required.)

CLICK THE TRIANGLES LINK AT THIS HOME PAGE

Cheers,

~ Mark