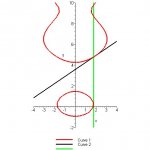
Here's the problem:
"Consider the curve defined by the implicit equation y+5cosy=x^2+2.
a) Find dy/dx in terms of x and y.
b) Find the equation of the tangent line at the point shown where x=2.
c) Find two positive values of x in the portion of the curve shown at which there is a vertical tangent line." (There's a picture here of the graph, given so that one could visually look to see where they think a vertical tangent line might be.) "Use calculus to find the values to 3 decimal places. You can use your calculator to solve the equation that must be true for a vertical tangent line."
Any help on how to solve these, please?
"Consider the curve defined by the implicit equation y+5cosy=x^2+2.
a) Find dy/dx in terms of x and y.
b) Find the equation of the tangent line at the point shown where x=2.
c) Find two positive values of x in the portion of the curve shown at which there is a vertical tangent line." (There's a picture here of the graph, given so that one could visually look to see where they think a vertical tangent line might be.) "Use calculus to find the values to 3 decimal places. You can use your calculator to solve the equation that must be true for a vertical tangent line."
Any help on how to solve these, please?