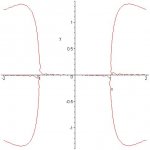
A curve xsin(xy)=y crosses the x-axis at two points (the image is reflected around the y-axis). At these two points of intersection the tangent line to the curve is vertical. Find the x-coordinate at each of the two points the curve crosses thed x-axis.
I'm stuck. I tried implicit differentation and got y'=sin(xy)/1-xcos(xy), then tried to substitute it into the equation 0=mx+b. Zero because the I'm looking for the x coorinate when y=0 and b=0. I keep getting x=0. Where am I going wrong? Did I not even start the problem correctly. I'm studying immplicit defferentiation.
Thanks
I'm stuck. I tried implicit differentation and got y'=sin(xy)/1-xcos(xy), then tried to substitute it into the equation 0=mx+b. Zero because the I'm looking for the x coorinate when y=0 and b=0. I keep getting x=0. Where am I going wrong? Did I not even start the problem correctly. I'm studying immplicit defferentiation.
Thanks