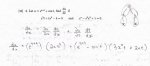You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Implicit differentiation - Multivariable calculus
- Thread starter chengeto
- Start date
Hello, chengeto!
Your formula is correct . . . your partial differentiation isn't.
\(\displaystyle \text{Formula: }\;\frac{du}{dx} \;=\;\frac{\partial u}{\partial s}\cdot\frac{ds}{dx} + \frac{\partial u}{\partial t}\cdot\frac{dt}{dx}\) .[1]
\(\displaystyle \text{We have: }\:\boxed{\begin{array}{ccc}\dfrac{\partial u}{\partial s} &=& e^{s+t} \\ \\[-3mm] \dfrac{\partial u}{\partial t} &=& e^{s+t} \end{array}}\) .[2]
\(\displaystyle \text{Differentiate (A) w.r.t. }x\!:\quad x^3\frac{dt}{dx} \;+\; 3x^2\;+\; x^2\frac{dt}{dx} \;+\; 2xt\:=\:0 \quad\Rightarrow\quad x^3\frac{dt}{dx} \;+\; x^2\frac{dt}{dx} \;=\;-(3x^2 \;+\; 2xt)\)
. . . . . . . . . . . . . . . . . . . \(\displaystyle x^2(x+1)\frac{dt}{dx} \;=\;-x(3x+2t) \quad\Rightarrow\quad \boxed{\frac{dt}{dx} \;=\;-\frac{3x+2t}{x(x+1)}}\) .[3]
\(\displaystyle \text{Differentiate (B) w.r.t. }x\!:\quad e^s\frac{ds}{dx}\;-\;3x^2s^2\frac{ds}{dx}\;-\;2xs^3 \;\;=\;\;0 \quad\Rightarrow\quad e^s\frac{ds}{dx}\;-\;3x^2s^2\frac{ds}{dx} \;\;=\;\;2xs^3\)
. . . . . . . . . . . . . . . . . . . . . . . . \(\displaystyle \left(e^x-3x^2s^2\right)\frac{ds}{dx} \;=\;2xs^3 \quad\Rightarrow\quad \boxed{\frac{ds}{dx} \;=\;\frac{2xs^2}{e^s-3x^2s^2}}\) .[4]
Substitute [2], [3], [4] into [1]:
. . \(\displaystyle \frac{du}{dx}\;\;=\;\;\left(e^{s+t}\right)\left[\frac{2xs^2}{e^s-3x^2s^2}\right] + \left(e^{s+t}\right)\left[-\frac{3x+2t}{x(x+1)}\right] \;\;=\;\;e^{s+t}\left[\frac{2xs^2}{e^s-3x^2s^2} - \frac{3x+2t}{x(x+1)}\right]\)
Your formula is correct . . . your partial differentiation isn't.
\(\displaystyle \text{3. Let: }\:u \;=\;e^{s+t}\:\text{ and }\:\begin{Bmatrix}x^3t + x^2t -4 &=& 0 & (A) \\ e^s - x^2s^3 + 1 &=& 0 & (B) \end{Bmatrix} \qquad \text{Find: }\:\frac{du}{dx}\)
\(\displaystyle \text{Formula: }\;\frac{du}{dx} \;=\;\frac{\partial u}{\partial s}\cdot\frac{ds}{dx} + \frac{\partial u}{\partial t}\cdot\frac{dt}{dx}\) .[1]
\(\displaystyle \text{We have: }\:\boxed{\begin{array}{ccc}\dfrac{\partial u}{\partial s} &=& e^{s+t} \\ \\[-3mm] \dfrac{\partial u}{\partial t} &=& e^{s+t} \end{array}}\) .[2]
\(\displaystyle \text{Differentiate (A) w.r.t. }x\!:\quad x^3\frac{dt}{dx} \;+\; 3x^2\;+\; x^2\frac{dt}{dx} \;+\; 2xt\:=\:0 \quad\Rightarrow\quad x^3\frac{dt}{dx} \;+\; x^2\frac{dt}{dx} \;=\;-(3x^2 \;+\; 2xt)\)
. . . . . . . . . . . . . . . . . . . \(\displaystyle x^2(x+1)\frac{dt}{dx} \;=\;-x(3x+2t) \quad\Rightarrow\quad \boxed{\frac{dt}{dx} \;=\;-\frac{3x+2t}{x(x+1)}}\) .[3]
\(\displaystyle \text{Differentiate (B) w.r.t. }x\!:\quad e^s\frac{ds}{dx}\;-\;3x^2s^2\frac{ds}{dx}\;-\;2xs^3 \;\;=\;\;0 \quad\Rightarrow\quad e^s\frac{ds}{dx}\;-\;3x^2s^2\frac{ds}{dx} \;\;=\;\;2xs^3\)
. . . . . . . . . . . . . . . . . . . . . . . . \(\displaystyle \left(e^x-3x^2s^2\right)\frac{ds}{dx} \;=\;2xs^3 \quad\Rightarrow\quad \boxed{\frac{ds}{dx} \;=\;\frac{2xs^2}{e^s-3x^2s^2}}\) .[4]
Substitute [2], [3], [4] into [1]:
. . \(\displaystyle \frac{du}{dx}\;\;=\;\;\left(e^{s+t}\right)\left[\frac{2xs^2}{e^s-3x^2s^2}\right] + \left(e^{s+t}\right)\left[-\frac{3x+2t}{x(x+1)}\right] \;\;=\;\;e^{s+t}\left[\frac{2xs^2}{e^s-3x^2s^2} - \frac{3x+2t}{x(x+1)}\right]\)
soroban said:Hello, chengeto!
Your formula is correct . . . your partial differentiation isn't.
\(\displaystyle \text{3. Let: }\:u \;=\;e^{s+t}\:\text{ and }\:\begin{Bmatrix}x^3t + x^2t -4 &=& 0 & (A) \\ e^s - x^2s^3 + 1 &=& 0 & (B) \end{Bmatrix} \qquad \text{Find: }\:\frac{du}{dx}\)
\(\displaystyle \text{Formula: }\;\frac{du}{dx} \;=\;\frac{\partial u}{\partial s}\cdot\frac{ds}{dx} + \frac{\partial u}{\partial t}\cdot\frac{dt}{dx}\) .[1]
\(\displaystyle \text{We have: }\:\boxed{\begin{array}{ccc}\dfrac{\partial u}{\partial s} &=& e^{s+t} \\ \\[-3mm] \dfrac{\partial u}{\partial t} &=& e^{s+t} \end{array}}\) .[2]
\(\displaystyle \text{Differentiate (A) w.r.t. }x\!:\quad x^3\frac{dt}{dx} \;+\; 3x^2\;+\; x^2\frac{dt}{dx} \;+\; 2xt\:=\:0 \quad\Rightarrow\quad x^3\frac{dt}{dx} \;+\; x^2\frac{dt}{dx} \;=\;-(3x^2 \;+\; 2xt)\)
. . . . . . . . . . . . . . . . . . . \(\displaystyle x^2(x+1)\frac{dt}{dx} \;=\;-x(3x+2t) \quad\Rightarrow\quad \boxed{\frac{dt}{dx} \;=\;-\frac{3x+2t}{x(x+1)}}\) .[3]
\(\displaystyle \text{Differentiate (B) w.r.t. }x\!:\quad e^s\frac{ds}{dx}\;-\;3x^2s^2\frac{ds}{dx}\;-\;2xs^3 \;\;=\;\;0 \quad\Rightarrow\quad e^s\frac{ds}{dx}\;-\;3x^2s^2\frac{ds}{dx} \;\;=\;\;2xs^3\)
. . . . . . . . . . . . . . . . . . . . . . . . \(\displaystyle \left(e^x-3x^2s^2\right)\frac{ds}{dx} \;=\;2xs^3 \quad\Rightarrow\quad \boxed{\frac{ds}{dx} \;=\;\frac{2xs^2}{e^s-3x^2s^2}}\) .[4]
Substitute [2], [3], [4] into [1]:
. . \(\displaystyle \frac{du}{dx}\;\;=\;\;\left(e^{s+t}\right)\left[\frac{2xs^2}{e^s-3x^2s^2}\right] + \left(e^{s+t}\right)\left[-\frac{3x+2t}{x(x+1)}\right] \;\;=\;\;e^{s+t}\left[\frac{2xs^2}{e^s-3x^2s^2} - \frac{3x+2t}{x(x+1)}\right]\)
Thanks