You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Implicit differentation
- Thread starter crouchjr
- Start date
- Joined
- Apr 12, 2005
- Messages
- 11,325
Step #1 Make sure the point is on the curve. Please demonstrate this.
Step #2 Use your Implicit Differentiation skills. This requires a nice understanding fo the Chain Rule
For the first term, I get -4x <== Just the good old polynomial rule there.
For the second term, I get -x*(dy/dx) - y <== A thing of beauty. Product rule and chain rule.
You do the third term and the other side of the equal sign.
Step #3 Find dy/dx
Step #4 Evaluate dy/dx at the given point (assuming it is on the curve).
Step #2 Use your Implicit Differentiation skills. This requires a nice understanding fo the Chain Rule
For the first term, I get -4x <== Just the good old polynomial rule there.
For the second term, I get -x*(dy/dx) - y <== A thing of beauty. Product rule and chain rule.
You do the third term and the other side of the equal sign.
Step #3 Find dy/dx
Step #4 Evaluate dy/dx at the given point (assuming it is on the curve).
BigGlenntheHeavy
Senior Member
- Joined
- Mar 8, 2009
- Messages
- 1,577
\(\displaystyle Given: \ -2x^{2}-xy-4y^{3}+110 \ = \ 0, \ and \ point(-2,3)\)
\(\displaystyle Find \ line \ tangent \ to \ f(x,y) \ at \ the \ point.\)
\(\displaystyle Implicit \ differentiation \ yields: \ -4x-[y+xy']-12y^{2}y'+0 \ = \ 0\)
\(\displaystyle -4x-y-xy'-12y^{2}y' \ = \ 0 \ \implies \ y' \ = \ -\frac{4x+y}{x+12y^{2}}, \ at \ (-2,3), \ m \ = \ \frac{5}{106}.\)
\(\displaystyle Hence, \ y-3 \ = \ \frac{5}{106}(x+2), \ y \ = \ \frac{5x+328}{106}.\)
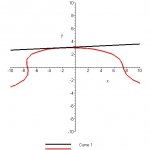
\(\displaystyle See \ graph.\)
[attachment=0:1gseb7b0]zero.jpg[/attachment:1gseb7b0]
\(\displaystyle Find \ line \ tangent \ to \ f(x,y) \ at \ the \ point.\)
\(\displaystyle Implicit \ differentiation \ yields: \ -4x-[y+xy']-12y^{2}y'+0 \ = \ 0\)
\(\displaystyle -4x-y-xy'-12y^{2}y' \ = \ 0 \ \implies \ y' \ = \ -\frac{4x+y}{x+12y^{2}}, \ at \ (-2,3), \ m \ = \ \frac{5}{106}.\)
\(\displaystyle Hence, \ y-3 \ = \ \frac{5}{106}(x+2), \ y \ = \ \frac{5x+328}{106}.\)
\(\displaystyle See \ graph.\)
[attachment=0:1gseb7b0]zero.jpg[/attachment:1gseb7b0]