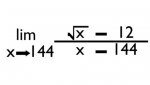I'm reaching the "limit" of my patience

[NRS]

I'm studying for a final, and there will be a problem very much like this one on it. I'm drawing a blank on how to get this answer, I keep getting an undefined answer, while I know the limit can be taken.
[attachment=0:3ntv6iq9]limprob.jpg[/attachment:3ntv6iq9]

 

[galactus]

Try rationalizing the numerator.

\(\displaystyle \frac{(\sqrt{x}-12)(\sqrt{x}+12)}{(x-144)(\sqrt{x}+12)}\)

\(\displaystyle \frac{x-144}{(\sqrt{x}+12)(x-144)}=\frac{1}{\sqrt{x}+12}\)

\(\displaystyle \lim_{x\to 144}\frac{1}{\sqrt{x}+12}\)

Now, want do you get?

 

[NRS]

how do you simplify the result of the multiplication in the denominator?

 

[NRS]

Aha! now I see the obvious The answer would be 1/24?

Thankyou very much!

 

[galactus]

Yep. The x-144 cancels and you just plug in x=144. Whenever you see a limit involving a radical like this one, think about rationalizing in the dnominator or numerator. Wherever it may be.

 

[chrisr]

or factorise the denominator to \(\displaystyle (\sqrt{x}-12)(\sqrt{x}+12)\).

 

[chrisr]

\(\displaystyle \lim_{x\to 144}\frac{\sqrt{x}-12}{x-144}=\lim_{x\to 144}\frac{\sqrt{x}-12}{(\sqrt{x}-12)(\sqrt{x}+12)}\).

The fraction's value is not defined at x=144 but the limit as x approaches 144 is.

 

[BigGlenntheHeavy]

Good show Chrisr, instead of rationalizing the numerator, you avoided a step by factoring the denominator.

 

[chrisr]

Thanks for the compliment Glenn,
I was answering a post that disappeared,
in any case I prefer salt and vinegar to cheese.

 

[Aladdin]

Thanks for the compliment Glenn,
I was answering a post that disappeared,
in any case I prefer salt and vinegar to cheese.

Don't worry , Chris :wink: