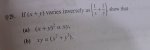VincentTong
New member
- Joined
- Feb 22, 2017
- Messages
- 2
29. If (x + y) varies inversely as \(\displaystyle \left(\dfrac{1}{x}\, +\, \dfrac{1}{y}\right)\) show that:
(a) \(\displaystyle (x\, +\, y)^2\, \propto\, xy\)
(b) \(\displaystyle xy\, \propto\, (x\, +\, y)^2\)
29. It is given that z varies directly as y when x is constant, and varies inversely as x when y is constant. Show that
. . .\(\displaystyle z\, \propto\, y^2\, \mbox{ if }\, y\, \propto\, \dfrac{1}{x}\)
I couldn't find the answer. The topic i was in is variations. And the Question 29 containing a and b i solved a but not b. Could i be answered?
(a) \(\displaystyle (x\, +\, y)^2\, \propto\, xy\)
(b) \(\displaystyle xy\, \propto\, (x\, +\, y)^2\)
29. It is given that z varies directly as y when x is constant, and varies inversely as x when y is constant. Show that
. . .\(\displaystyle z\, \propto\, y^2\, \mbox{ if }\, y\, \propto\, \dfrac{1}{x}\)
I couldn't find the answer. The topic i was in is variations. And the Question 29 containing a and b i solved a but not b. Could i be answered?
Attachments
Last edited by a moderator: