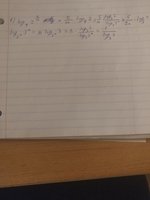I got stuck. Almost done

[Soracyn11]

Number 8.

Here is my work as well. We have the 5/2 term. I have a question does the LHS before the sqrt32 term equal log base 2^n of 3^n?

 

[Dr.Peterson]

I would definitely express the LHS in terms of [MATH]log_2[/MATH], since the bases are all powers of 2. But do you see that [MATH]log_{2^n}\left(3^n\right) = log_2(3)[/MATH]? That isn't quite what the first (parenthesized) part of the LHS is.

The first line of your work looks correct, though it would be simpler if you used [MATH]log_2[/MATH] as I recommend.

 

[Soracyn11]

How do those terms equal?

 

[Dr.Peterson]

Use the change of base formula! What else?

[MATH]\log_{2^n}\left(3^n\right) = \frac{\log_2{3^n}}{\log_2{2^n}} = \frac{n \log_2{3}}{n \log_2{2}} = \frac{\log_2{3}}{\log_2{2}} = \log_2(3)[/MATH]​

This is the kind of work I've suggested doing almost everywhere.

 

[Soracyn11]

I got 5/2n = 5/2 which does not equal. :/

 

[Steven G]

In the left attachment I would not leave what you have in the 2nd line as your final result. Write that answer with the log in the numerator.

 

[Steven G]

a^2 + b^2 = c^2 --> c^2 -b^2 = a^2 ---> (c+b)(c-b) = a^2

log_(c+b)[(c+b)(c-b)] = 2log_(c+b)a

log_(c+b)(c+b) + log_(c+b)(c-b) = 2log_(c+b)a

You need to make this work! If we multiply both sides by log_(c-b)a then the rhs is exactly what we want. So let's do this.

log_(c-b)a *(log_(c+b)(c+b) + log_(c+b)(c-b)) = 2log_(c+b)alog_(c-b)a

log_(c-b)a log_(c+b)(c+b) + log_(c-b)a log_(c+b)(c-b) = 2log_(c+b)alog_(c-b)a

log_(c-b)a +log_(c+b)a = 2log_(c+b)alog_(c-b)a

 

[Dr.Peterson]

I got 5/2n = 5/2 which does not equal. :/

Your work on the parenthesized part is wrong.

Have you tried applying what I showed in #4 to each term?

[MATH]\log_{2^n}\left(3^n\right) = \frac{\log_2{3^n}}{\log_2{2^n}} = \frac{n \log_2{3}}{n \log_2{2}} = \frac{\log_2{3}}{\log_2{2}} = \log_2(3)[/MATH]
This is the kind of work I've suggested doing almost everywhere.

Do it! I think you'll be surprised!

 

[Dr.Peterson]

a^2 + b^2 = c^2 --> c^2 -b^2 = a^2 ---> (c+b)(c-b) = a^2

log_(c+b)[(c+b)(c-b)] = 2log_(c+b)a

log_(c+b)(c+b) + log_(c+b)(c-b) = 2log_(c+b)a

You need to make this work! If we multiply both sides by log_(c-b)a then the rhs is exactly what we want. So let's do this.

log_(c-b)a *(log_(c+b)(c+b) + log_(c+b)(c-b)) = 2log_(c+b)alog_(c-b)a

log_(c-b)a log_(c+b)(c+b) + log_(c-b)a log_(c+b)(c-b) = 2log_(c+b)alog_(c-b)a

log_(c-b)a +log_(c+b)a = 2log_(c+b)alog_(c-b)a

This thread has been about problem 8, not 9. I think this belongs in a different thread.

 

[pka]

This thread has been about problem 8, not 9. I think this belongs in a different thread.

More reason to have guidelines for images.