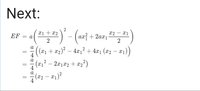So my question is concerning Archimedes' Quadrature of Parabola.
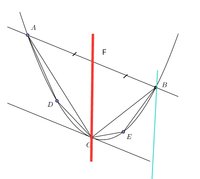
In his theorem I understand everything except for why the area of [MATH] ∆ACD [/MATH] and [MATH]∆CEB[/MATH] is [MATH]1/8×S∆ABC[/MATH]. So I decided to try to prove it.
All I know is that C is a midpoint between A and B. Tangent to C is parallel to AB. I also tried to drop a line from point B, parallel to FC but I'm still stuck.
Any hints will be hugely appreciated!
In his theorem I understand everything except for why the area of [MATH] ∆ACD [/MATH] and [MATH]∆CEB[/MATH] is [MATH]1/8×S∆ABC[/MATH]. So I decided to try to prove it.
All I know is that C is a midpoint between A and B. Tangent to C is parallel to AB. I also tried to drop a line from point B, parallel to FC but I'm still stuck.
Any hints will be hugely appreciated!