maggiegold
New member
- Joined
- Jan 23, 2021
- Messages
- 5
Older post reference:
I am given this question- I'm stuck with using programming to solve discretion problems
For Question 1a), I am given that
The governing equation for the temperature distribution with time on a 2D square plate measuring 1 unit by1 unit is
∂T/∂t = ∂2T/∂x2 + ∂2T/∂y2 ,
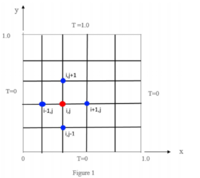
subjected to the Dirichlet boundary conditions for T provided in Fig.1.
I am supposed to obtain the temperature contour plot on the square plate with time, say at t=0.01, 0.1 and at steady state.
For Question 1b), I am given that
∂2T/∂x2 + ∂2T/∂y2 = 0,
Question Requirement:
Question 1a) Express Tij @ t+1 = F(Ti+1,j, Ti-1,j, Ti,j+1, Ti,j-1 at t explicitly, then advance in time
Question 1b)
Suppose, there is no t variable, now what? Make a guess!
Ideally: F(Ti,j, Ti+1,j , Ti-1,j, Ti,j+1, Ti,j-1)=0
With guessed values: F(Ti,j, Ti+1,j , Ti-1,j, Ti,j+1, Ti,j-1)= err(/=0)
Objective is to reduce error as much as possible
Requirements
Write down discretized equations(interior, boundary)- explicit, implicit?
Specify what algorithms are used and how to program?

Question on Numerical methods- How do I use programming to solve discretion problems?
I am given this question- I'm stuck with using programming to solve discretion problems Question 1a) Express Tij @ t+1 = F(Ti+1,j, Ti-1,j, Ti,j+1, Ti,j-1) at t explicitly, then advance in time Question 1b) Suppose, there is no t variable, now what? Make a guess! Ideally: F(Ti,j, Ti+1,j , Ti-1,j...
www.freemathhelp.com
I am given this question- I'm stuck with using programming to solve discretion problems
For Question 1a), I am given that
The governing equation for the temperature distribution with time on a 2D square plate measuring 1 unit by1 unit is
∂T/∂t = ∂2T/∂x2 + ∂2T/∂y2 ,
subjected to the Dirichlet boundary conditions for T provided in Fig.1.
I am supposed to obtain the temperature contour plot on the square plate with time, say at t=0.01, 0.1 and at steady state.
For Question 1b), I am given that
∂2T/∂x2 + ∂2T/∂y2 = 0,
Question Requirement:
Question 1a) Express Tij @ t+1 = F(Ti+1,j, Ti-1,j, Ti,j+1, Ti,j-1 at t explicitly, then advance in time
Question 1b)
Suppose, there is no t variable, now what? Make a guess!
Ideally: F(Ti,j, Ti+1,j , Ti-1,j, Ti,j+1, Ti,j-1)=0
With guessed values: F(Ti,j, Ti+1,j , Ti-1,j, Ti,j+1, Ti,j-1)= err(/=0)
Objective is to reduce error as much as possible
Requirements
Write down discretized equations(interior, boundary)- explicit, implicit?
Specify what algorithms are used and how to program?

Attachments
Last edited by a moderator: