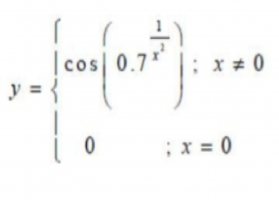I am struggling in classification of discontinuities

P

pineapplewithmouse

Junior Member
Joined
Jun 22, 2021
Messages
52
I have the function y (in the picture)
I need to find what type of discontinuity the function has.
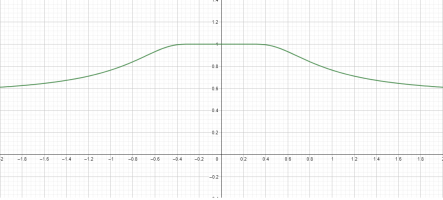
When I draw the graph it seems like this is a jump discontinuity because the graph goes from almost y=1 straight to y=0 and then again to almost y=1.
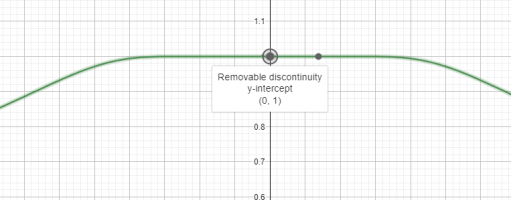
But when I check the limits to 0+ and 0- there are the same, meaning this is a removable discontinuity.
What is the right one?
 

Attachments

  • function.png
    function.png
    60.5 KB · Views: 7
pineapplewithmouse said:
I have the function y (in the picture)
I need to find what type of discontinuity the function has.
When I draw the graph it seems like this is a jump discontinuity because the graph goes from almost y=1 straight to y=0 and then again to almost y=1.
But when I check the limits to 0+ and 0- there are the same, meaning this is a removable discontinuity.
What is the right one?
Click to expand...
Please show us your graph, so we can talk about it.
 
pineapplewithmouse said:
Nevermind, I understood my mistake
Thanks for trying to help
Click to expand...
I presume you see that "jumping" down to 0 and then back up to the same place makes a removable discontinuity. I figured that trying to show it would make it visible to you.

It's a little harder when you don't use technology, but even an inaccurate graph can give you the idea.
 
pineapplewithmouse said:
It's a removable discontinuity?
But x=0 is defined, why it has a discontinuity
Click to expand...
You think it isn't a discontinuity? Please state the definition you were taught, and how you think that applies. You seemed to have said the right things initially! (This is why we like to see your answer, not just a claim that you are finished!)

Here's a better version of the graph:

1660576277032.png​

1660576215894.png​
 
Weird. as I showed, Geogebra didn't show the discontinuity point when it usually does.
I was taught that lim(x->a+)=lim(x->a-) means removable discontinuity
and lim(x->a+)≠lim(x->a-) means jump discontinuity

Let me express my logic:
The function cos(0.7^1/x^2) has removable discontinuity in x=0
But the definition of f(x) states that we need to draw this function only when x≠0 so we need to ignore the removable discontinuity because it's not a part of the function.
So we have a "hole" in x=0, but the second function in f(x) fills up the "hole".
So now we have no "holes" and no discontinuities, hence f(x) has no discontinuities.
Why my logic is wrong?

And you also said "I presume you see that "jumping" down to 0 and then back up to the same place makes a removable discontinuity"
Why? In the cos function you put numbers that are not equal to 0, so:
When you input in the cos function positive infinitesimal number (0+) the limit is 1
When you input in the cos function negative infinitesimal number (0-) the limit is 1
And when you input x=0 into f(x) you get 0.
So the limits are not equal, so there is a jump discontinuity

(I know I am saying things that are conflicting with each other, I am just saying mine and my friend's logic about the problem, and I just want to understand where each of us are wrong)
 
This is a matter of definition. f(x) is continuous at a if and only if

[math]\lim_{x \rightarrow a^-} f(x) = f(a) = \lim_{x \rightarrow a^+} f(x).[/math]
Three things must be equal rather than just two.

We say a discontinuity is “removable” if we can adjust the definition of f(x) to g(x) so that g(x) = f(x) almost everywhere and so that

[math]\lim_{x \rightarrow a^-} f(x) = \lim_{x \rightarrow a^-} g(x) = g(a) = \lim_{x \rightarrow a^+} g(x) = \lim_{x \rightarrow a^+} f(x).[/math]
A removable discontinuity is one that can be eliminated by a minor tweak to the definition of the function.

Here is an example

[math]f(x) = \dfrac{\sin(x)}{x} \text { if } x \ne 0.\\ g(x) = \dfrac{\sin(x)}{x} \text { if } x \ne 0, \text { but } g(x) = 1 \text { if } x = 0.[/math]
Here is another example

[math]f(x) = \dfrac{x^3 - 1}{x - 1} \text { if } x \ne 1.\\ g(x) = x^2 + x + 1 \text { for all } x.[/math]
We can alter the function to eliminate the discontinuity without affecting the meaning of the function elsewhere.
 
Last edited:
pineapplewithmouse said:
Weird. as I showed, Geogebra didn't show the discontinuity point when it usually does.
Click to expand...
I had to intentionally add the two dots on Desmos. In general, I don't expect any program to handle discontinuities well. But how did you enter this piecewise function into GeoGebra? I'd like to see that. I know it doesn't show holes, at least not typically.

In any case, never depend on technology to show you the whole truth -- or the "hole truth"!
pineapplewithmouse said:
I was taught that lim(x->a+)=lim(x->a-) means removable discontinuity
and lim(x->a+)≠lim(x->a-) means jump discontinuity
Click to expand...
This incomplete; presumably you are also checking f(a).
pineapplewithmouse said:
Let me express my logic:
The function cos(0.7^1/x^2) has removable discontinuity in x=0
But the definition of f(x) states that we need to draw this function only when x≠0 so we need to ignore the removable discontinuity because it's not a part of the function.
So we have a "hole" in x=0, but the second function in f(x) fills up the "hole".
So now we have no "holes" and no discontinuities, hence f(x) has no discontinuities.
Why my logic is wrong?
Click to expand...
But the second part of the piecewise function doesn't "fill" the hole; it has a different value, as shown in my graph. (It's like "filling" a pothole by putting a lump of asphalt on the other side of the road.) Doesn't that graph make that extremely clear?

And if you made the graph by hand (as I partly did!), that would make it even clearer.
pineapplewithmouse said:
And you also said "I presume you see that "jumping" down to 0 and then back up to the same place makes a removable discontinuity"
Why? In the cos function you put numbers that are not equal to 0, so:
When you input in the cos function positive infinitesimal number (0+) the limit is 1
When you input in the cos function negative infinitesimal number (0-) the limit is 1
And when you input x=0 into f(x) you get 0.
So the limits are not equal, so there is a jump discontinuity
Click to expand...
But you yourself said, "lim(x->a+)≠lim(x->a-) means jump discontinuity". That is not true here. The limits are equal; it is the value that is not. Since that is precisely what I said was missing in your definition, perhaps you need to recheck the definitions you were taught.
 
Dr.Peterson said:
But how did you enter this piecewise function into GeoGebra?
Click to expand...
If(x≠0, cos(0.7^(((1)/(x^(2))))), 0)
If you will write just the cos(0.7^(((1)/(x^(2))))) it will show a removable discontinuity

Dr.Peterson said:
This incomplete; presumably you are also checking f(a).
Click to expand...
Didn't know that
Dr.Peterson said:
But the second part of the piecewise function doesn't "fill" the hole; it has a different value, as shown in my graph. (It's like "filling" a pothole by putting a lump of asphalt on the other side of the road.) Doesn't that graph make that extremely clear?
Click to expand...
By saying "filling up" I meant giving a value to something that doesn't have a value, not literally fill up the hole in the graph

Dr.Peterson said:
But you yourself said, "lim(x->a+)≠lim(x->a-) means jump discontinuity". That is not true here. The limits are equal; it is the value that is not. Since that is precisely what I said was missing in your definition, perhaps you need to recheck the definitions you were taught.
Click to expand...
I understand it now with the f(a) thing, thanks
 
pineapplewithmouse said:
Didn't know that

By saying "filling up" I meant giving a value to something that doesn't have a value, not literally fill up the hole in the graph

I understand it now with the f(a) thing, thanks
Click to expand...
Here is a typical textbook presentation of these ideas. I hope your own is similar.

pineapplewithmouse said:
If(x≠0, cos(0.7^(((1)/(x^(2))))), 0)
If you will write just the cos(0.7^(((1)/(x^(2))))) it will show a removable discontinuity
Click to expand...
Interesting. I have been using a somewhat old downloaded version, which doesn't show the discontinuity at all; I see that the online version shows it as

1660583937678.png​

which to me is misleading, as the gap is rather large. But you're right that the piecewise formula shows no discontinuity on either version of GeoGebra. You need to check what any software does against your own reasoning; it should have bothered you that it didn't show a point (0,0).
 
pineapplewithmouse said:
This is what I get when I write the function
Very interesting
Click to expand...

There are several versions of GeoGebra. Please be very specific about what you are using -- the address you use and how you open it. I haven't explored these options at all; maybe someone else here has more knowledge of them.
 
That's even more odd. I did the same thing before, but now I see what you saw. I don't know what was different.

In any case, now you know, as I already knew, that you can't depend on software to do all the thinking for you. And I know a little more about GeoGebra than I did.
 
You must log in or register to reply here.
Top