Ok, you'll have to set this one up yourself because I can't seem to copy and paste my figure into this space:
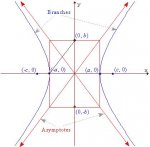
Hyperbola opens left and right.
Center (0,0)
foci (-c,0), (+c,0)
Vertices (-a, 0), (+a,0)
The transverse axis is 2a and the conjugate axis is 2b
The distance from the center to the endpoint on the conjugate axis is b.
The distance from the center to a vertex is a.
The distance from a vertex to the endpoint of the conjugate axis (hypotenuse of the right triangle) is sqrt (a[sup:2s7xz8e9]2[/sup:2s7xz8e9]+ b[sup:2s7xz8e9]2[/sup:2s7xz8e9]) which is somehow equal to the distance from the center to the focus which is c. How is that? How do I know that c[sup:2s7xz8e9]2[/sup:2s7xz8e9] = a[sup:2s7xz8e9]2[/sup:2s7xz8e9] + b[sup:2s7xz8e9]2[/sup:2s7xz8e9] in this context?
Hope you can either draw the picture or produce one for reference. Thanks. Dale
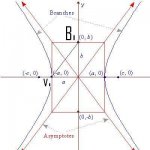
Hyperbola opens left and right.
Center (0,0)
foci (-c,0), (+c,0)
Vertices (-a, 0), (+a,0)
The transverse axis is 2a and the conjugate axis is 2b
The distance from the center to the endpoint on the conjugate axis is b.
The distance from the center to a vertex is a.
The distance from a vertex to the endpoint of the conjugate axis (hypotenuse of the right triangle) is sqrt (a[sup:2s7xz8e9]2[/sup:2s7xz8e9]+ b[sup:2s7xz8e9]2[/sup:2s7xz8e9]) which is somehow equal to the distance from the center to the focus which is c. How is that? How do I know that c[sup:2s7xz8e9]2[/sup:2s7xz8e9] = a[sup:2s7xz8e9]2[/sup:2s7xz8e9] + b[sup:2s7xz8e9]2[/sup:2s7xz8e9] in this context?
Hope you can either draw the picture or produce one for reference. Thanks. Dale