Hyperbola problem

[spray]

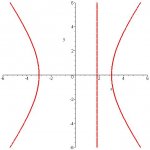
The distance between a point P(x,y) and the point (5,0) is 5/3 of the distance between P and the line x=9/5

Write the hyperbola, in standard form, of all such points.

I have gotten that a^2=9 and that b^2=16. What I don't know though is how to correctly put that into standard form. Is it
( x^2 / 9 ) - ( y^2 / 16 ) = 1
or
( y^2 / 9 ) - ( x^2 / 16 ) = 1

 

[BigGlenntheHeavy]

$\displaystyle \sqrt((x-5)^{2}+(y-0)^{2}) \ = \ \frac{5}{3}\bigg(x-\frac{9}{5}\bigg)$

$\displaystyle (x-5)^{2}+y^{2} \ = \ \frac{25}{9}\bigg(x-\frac{9}{5}\bigg)^{2}$

$\displaystyle x^{2}-10x+25+y^{2} \ = \ \frac{25}{9}\bigg(x^{2}-\frac{18x}{5}+\frac{81}{25}\bigg)$

$\displaystyle x^{2}-10x+25+y^{2} \ = \ \frac{25x^{2}}{9}-10x+9$

$\displaystyle \frac{25x^{2}}{9}-\frac{9x^{2}}{9}-y^{2} \ = \ 25-9$

$\displaystyle \frac{16x^{2}}{9}-y^{2} \ = \ 16$

$\displaystyle \frac{x^{2}}{3^{2}}-\frac{y^{2}}{4^{2}} \ = \ 1, \ see \ graph$

[attachment=0:18tdphwo]abc.jpg[/attachment:18tdphwo]

 

[spray]

Thank you.