hydrostatic force

[mathstresser]

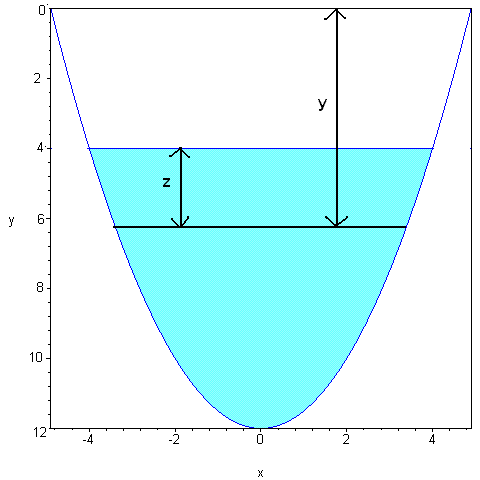
A large tank is designed with ends in the shape of the region between the curves y=(x-squared)/2 and y=12, measured in feet. Find the hydrostatic force on one end of the tank if it is filled to a depth of 8 ft with gasoline. (Assume the gasoline's density is 42 lb/cubic feet.)

I found the volume of the slice is ((x^2)/2)(8-x)(dx). 8-x is the depth.

Then I take that times the density and gravity.

(42)(9.8)(1/2)(x^2)(dx)= 205.8(8x^2-x^3)dx

Which I then make an integral and evaluate it from 0 to 8.

205.8((8/3)x^3-((1/4)x^4) evaluated from 0 to 8.

I get 70246.4.

I don't know what the answer should be, but this seems too high. What did I do wrong?

 

[Unco]

I'm having difficulty seeing how the depth can be 8-x. If you could explain it to me; all is swell.

This is what I, having read some material this morning, am thinking.

Weight density: \(\displaystyle \mbox{ \delta = \rho \cdot g = 42 \cdot 9.8 = 411.6}\)

Depth: \(\displaystyle \mbox{z = y - 4}\)

Width: \(\displaystyle \mbox{ y = \frac{x^2}{2} \Rightarrow x = \sqrt{2y}}\) so \(\displaystyle \mbox{w = 2\sqrt{2y}}\)

So force: \(\displaystyle \mbox{ F = \int^12_4 411.6 \cdot 2\sqrt{2y}(y - 4) dy}\)

I'm hungry and my head hurts, but I'm posting this despite.

 

[mathstresser]

I set my y-axis to go up and positive... and the problem said it was filled to a depth of 8 feet. That's why I think my depth= 8-y.

Thank you for your help.

 

[happy]

mathstresser, I like your turnaround from last night. Keep it up! :wink:

 

[mathstresser]

What do you mean?