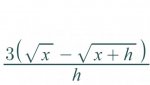Let \(\displaystyle \,f(x)\, =\, -7\, -\, 3\, \sqrt{\strut x\,}.\,\) Then the expression
. . . . .\(\displaystyle \dfrac{f(x\, +\, h)\, -\, f(x)}{h}\)
can be written in the form
. . . . .\(\displaystyle \dfrac{A}{\left(\sqrt{\strut Bx\, +\, Ch\,}\,\right)\, +\, \left(\sqrt{\strut x\,}\,\right)},\)
where A, B, and C are constants. Find the values of A, B, and C.
I have managed to change f(x) into the one required with all the h's and have simplified it by rationalizing the numerator. This is the fraction I got:
. . . . .\(\displaystyle \dfrac{3\, \left(\sqrt{\strut x\,}\, -\, \sqrt{\strut x\, +\, h\,}\right)}{h}\)
But I am not sure how to change it into the required form asked in the question above and am therefore unable to find the values of A, B and C.
So if anybody could be so kind to say whether or not my fraction above is correct, and, if so, how I should proceed, I would be deeply grateful.
Thank you!
. . . . .\(\displaystyle \dfrac{f(x\, +\, h)\, -\, f(x)}{h}\)
can be written in the form
. . . . .\(\displaystyle \dfrac{A}{\left(\sqrt{\strut Bx\, +\, Ch\,}\,\right)\, +\, \left(\sqrt{\strut x\,}\,\right)},\)
where A, B, and C are constants. Find the values of A, B, and C.
I have managed to change f(x) into the one required with all the h's and have simplified it by rationalizing the numerator. This is the fraction I got:
. . . . .\(\displaystyle \dfrac{3\, \left(\sqrt{\strut x\,}\, -\, \sqrt{\strut x\, +\, h\,}\right)}{h}\)
But I am not sure how to change it into the required form asked in the question above and am therefore unable to find the values of A, B and C.
So if anybody could be so kind to say whether or not my fraction above is correct, and, if so, how I should proceed, I would be deeply grateful.
Thank you!
Attachments
Last edited by a moderator: