How to simplify equation ?

[engineer88]

Hello,

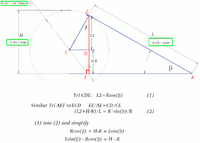
For my work I need to solve the following equation for [MATH]b[/MATH]. Normal euquation solver software can solve the equation, however since I need to calculate [MATH]b[/MATH] in a simple programming language (iLogic in Autodesk Inventor c.q. VBA) the equation should be simplified. I cannot find how to solve for [MATH]b[/MATH]. Can anyone help me?

[MATH]cos\left(b\right)\cdot \:L+cos\left(b\right)\cdot \sqrt{^{\frac{1}{sin\left(b\right)}^2-1}}\cdot \:R-H+R=\frac{R}{sin\left(b\right)}[/MATH]
Thanks!

 

[tkhunny]

"Simplify" is not an exact science.

Can you solve for [math]\dfrac{1}{\sin(b)}[/math] ?

 

[engineer88]

"Simplify" is not an exact science.

Can you solve for [math]\dfrac{1}{\sin(b)}[/math] ?

I understand what you mean.

Maybe I should explain more. Should this be the wrong forum, please let me know.

I have the following sketch:


The parameters with the green border are known. What I want to know is either the angle (d37) or the height difference (d38), the dimensions with the red box.


What I already found:
[MATH]beta = 90 - angle[/MATH]
[MATH]cos(beta)=\dfrac{Height + y}{Length + x}[/MATH]
[MATH]sin(beta)=\dfrac{H1}{Radius}[/MATH]
[MATH]cos(beta)=\dfrac{L1}{Radius}[/MATH]
[MATH]csc(beta)=\dfrac{H2}{Radius}[/MATH]
[MATH]y=H2-Radius=csc(beta)*Radius-Radius[/MATH]
[MATH]x=cot(beta)*Radius[/MATH]
So
[MATH]cos(beta)=\dfrac{Height + y}{Length + x}=\dfrac{Height + csc(beta)*Radius-Radius}{Length + cot(beta)*Radius}[/MATH]
That I rewrote to the equation in my op.

It must be possible to calculate the angle or height, right?

 

[Dr.Peterson]

Not everything can be calculated in closed form, but this can, I think.

I want to check your geometry, but starting with your final equation in this last post,

[MATH]cos(beta)=\dfrac{Height + y}{Length + x}=\dfrac{Height + csc(beta)*Radius-Radius}{Length + cot(beta)*Radius}[/MATH]​

which I will write as

[MATH]\cos(\beta)=\dfrac{H - R + R\csc(\beta)}{L + R\cot(\beta)}[/MATH]​

you can solve for [MATH]\beta[/MATH] by multiplying through by the denominator, then by [MATH]\sin(\beta)[/MATH] and simplifying in terms of sine and cosine. A little more manipulation got me to (if I didn't make a mistake)

[MATH]L\cos(\beta) - R\sin(\beta) = H - R[/MATH]​

There are a couple ways to solve this, one being to rewrite the LHS as a single cosine.

Again, I'll have to check for errors, either yours or mine!

 

[Cubist]

[MATH]L\cos(\beta) - R\sin(\beta) = H - R[/MATH]​

I've verified this equation starting from the diagram (not using engineer88's equations).
One thing to note is β=90^o - d37 (obviously swap sin <-> cos for β=d37)

My method is attached if you're interested, using similar triangles avoided some work

 

[Cubist]

Just to finish off (having swapped sin and cos so that β matches the diagram) ...

[math] \sqrt{R^2+L^2}\cdot \sin\left(\beta-\tan^{-1}\left(\frac{R}{L}\right)\right)=H-R [/math]

[math] \sin\left(\beta-\tan^{-1}\left(\frac{R}{L}\right)\right)=\frac{H-R}{\sqrt{R^2+L^2}} [/math]

[math] \beta=\sin^{-1}\left(\frac{H-R}{\sqrt{R^2+L^2}}\right)+\tan^{-1}\left(\frac{R}{L}\right) [/math]

 

[tkhunny]

[math] \beta=\sin^{-1}\left(\frac{H-R}{\sqrt{R^2+L^2}}\right)+\tan^{-1}\left(\frac{R}{L}\right) [/math]

Let's just be careful about the usage of inverse sine and inverse tangent.

Will you be happy with results in [math](-\pi/2,0][/math]?

Make sure your numeric implementation matches your theoretical conclusions.

 

[engineer88]

Just to finish off (having swapped sin and cos so that β matches the diagram) ...

[math] \sqrt{R^2+L^2}\cdot \sin\left(\beta-\tan^{-1}\left(\frac{R}{L}\right)\right)=H-R [/math]

[math] \sin\left(\beta-\tan^{-1}\left(\frac{R}{L}\right)\right)=\frac{H-R}{\sqrt{R^2+L^2}} [/math]

[math] \beta=\sin^{-1}\left(\frac{H-R}{\sqrt{R^2+L^2}}\right)+\tan^{-1}\left(\frac{R}{L}\right) [/math]

Cool! Thank you very much.

I came to a different result, using the abc-formula, where I replaced [MATH]cos(\beta) = u[/MATH]. With
[MATH]a = R^2 + L^2[/MATH][MATH]b = 2 * R * (H - R)[/MATH][MATH]c = (H - R)^2 - L^2[/MATH]
So [MATH]u = \frac{-b + \sqrt{b^2 - 4ac}}{2a}[/MATH]
[MATH]\beta = cos^{-1}(u)[/MATH]
The results are correct. And with this formula I can relatively easily go back to calculate [MATH]H[/MATH].

 

[Cubist]

I'm glad we've helped with your problem, engineer88.


tkhunny was right that some results were missing from my post #6

It seems better to use inverse cos instead of inverse sin, because then the missing results can be easily obtained with a ±.

Also, the inverse tan can be made more robust by using atan2 which is a quadrant-aware version of inverse tan available in many programming languages. Although in this case I think engineer88 will always have R>0 and L>0.

[math] \beta = \pm{\cos^{-1}\left(\frac{H-R}{\sqrt{L^2+R^2}}\right)}+\operatorname{atan2}\left(L,-R\right) [/math]
See the image, the green lines were previously missing ( obtained with the +ve option of the ± )


(constant H & R, different values of L)