I have a problem with the following question:
Q: What is the set of values of p for which p(x^2+2) < 2x^2+6x+1 for all real values of x?
My working is as follows:
First, just expand the left-hand side of the inequality,
px^2 + 2 p <
Q: What is the set of values of p for which p(x^2+2) < 2x^2+6x+1 for all real values of x?
My working is as follows:
First, just expand the left-hand side of the inequality,
px^2 + 2 p <
2x^2 + 6x + 1
Then, rearrange it to:
(2 - p)x^2 + 6x + 1 - 2p > 0
The determinant b^2 - 4ac = 6^2 - 4(2 - p)(1 - 2p)
= 36 - 4(2p^2 - 5p + 2)
= - 8 p^2 + 20 p + 28 >(or =) 0
So
2p^2 - 5p - 7 < (or =) 0
So
(2p - 7)(p + 1) < (or = )0
Therefore, - 1 < (or=) p < (or=) 7/2
However, I know that this working cannot be right because this is just a working to determine the range of p where x are real values, and it does not really mean that the left-hand side of the inequality is always less than the right-hand side of it.
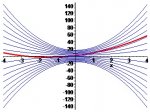
In fact, when p = 1, the left-hand side would be x^2 + 2, and you could clearly see that x^2 + 2 is not always below the curve of
And the answer provided by the text says that the right answer is:
p < - 1
&
p > 7/2
It looks like this answer comes from exactly the same way as I did as above (the differences are that it does not have "=" sign, which I do not understand why, and the range is totally opposite (complement) of my answer).
Having said that, this answer provided in the textbook does not seem to be correct, either.
Because, for example, when p = 4, which is more than 7/2, the left-hand side of the inequality would be 4x^2 + 8, and you could clearly see that it is actually more than
I have been very confused about this question as well as the answer provided in the book, and I would much appreciate it if someone can help me to find out the right solution for this question.
(By the way, we are not allowed to use a graphing calculator for this question. I just used the online graphing calculator to check both my and the book's answers)
Then, rearrange it to:
(2 - p)x^2 + 6x + 1 - 2p > 0
The determinant b^2 - 4ac = 6^2 - 4(2 - p)(1 - 2p)
= 36 - 4(2p^2 - 5p + 2)
= - 8 p^2 + 20 p + 28 >(or =) 0
So
2p^2 - 5p - 7 < (or =) 0
So
(2p - 7)(p + 1) < (or = )0
Therefore, - 1 < (or=) p < (or=) 7/2
However, I know that this working cannot be right because this is just a working to determine the range of p where x are real values, and it does not really mean that the left-hand side of the inequality is always less than the right-hand side of it.
In fact, when p = 1, the left-hand side would be x^2 + 2, and you could clearly see that x^2 + 2 is not always below the curve of
2x^2 + 6x + 1
if you check it using a graphing calculator.And the answer provided by the text says that the right answer is:
p < - 1
&
p > 7/2
It looks like this answer comes from exactly the same way as I did as above (the differences are that it does not have "=" sign, which I do not understand why, and the range is totally opposite (complement) of my answer).
Having said that, this answer provided in the textbook does not seem to be correct, either.
Because, for example, when p = 4, which is more than 7/2, the left-hand side of the inequality would be 4x^2 + 8, and you could clearly see that it is actually more than
2x^2 + 6x + 1
all the time for the same value of x, not less than the right-hand side of the inequality!I have been very confused about this question as well as the answer provided in the book, and I would much appreciate it if someone can help me to find out the right solution for this question.
(By the way, we are not allowed to use a graphing calculator for this question. I just used the online graphing calculator to check both my and the book's answers)