How to calculate angle in corner perspective?

[leo12345]

Hello!

I've been extensively searching in the internet and have not found the answer to this (as I thought) simple question.
Was I wrong and the question is not simple at all, and if so why?

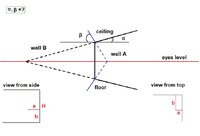
I am sitting in a room against the corner of two walls: wall A and wall B, and I am closer to wall A (see attached file).
I am drawing the corner: vertical line, two lines of the floor that cross somewhere with the vertical line and two lines of the ceiling that also cross the vertical line somewhat higher.
I know my distance from each of the walls and I know the height of the room and I know the distance from my eyes to the floor.
How do I calculate the angles Alpha and Beta between the lines on my drawing?

Kind regards,
Leo

 

[Dr.Peterson]

This will require a fairly solid understanding of what perspective means; it would take more work for me to work out than it is worth, though I have a feel for the basic concepts. I don't know what sites you've looked at, but I'd back out from the specific problem and try to get a larger perspective on the fundamentals (puns intended), if you haven't already done so. This looks like a basic problem in two-point perspective, so that might be where you want to focus. I did a quick search for fairly comprehensive sources; here are a couple that look potentially useful:

Mathematics of Perspective Drawing

http://www.sfu.ca/~rpyke/perspective.pdf

I don't think I've seen anything that talks explicitly about angles such as you are asking for; in part, that is because you don't generally use those angles to construct a drawing, but they would arise out of other things you do, and could be calculated as a last step.

Is there a specific reason you want these angles? Are you able otherwise to do the constructions? If you have, then show us what you do to construct the image, and we can perhaps help you find the angles from that.

 

[leo12345]

Thanks for your reply! I am an amateur drawer and I am familiar with the principles of perspective used in drawing. But I like math and I was interested in the problem - if the angles can be calculated. I was just puzzled by the fact that this is never mentioned elsewhere in the internet.

The principles of perspective drawing are simple:
(1) you have the "horizon" - horizontal line at the level of your eyes
(2) All lines parallel to the horizon remain such in the drawing
(3) All vertical lines remain such in the drawing
(4) All other parallel lines converge to some point on the "horizon" line. So if you have the corner of the room, like in the attached file, two lines connecting the wall A with floor and ceiling converge into a point on the horizon, two lines of wall B converge into another point on the horizon.

But the question is: where exactly does those point lie? In drawing you always define the point where your parallel lines converge (or the angle of convergence) approximately, just "by eye", without doing precise measurements. You normally hold a pencil in your outstretched hand and you "coincide" the pencil with the line you see and this way you "decide" the inclination of your line on the paper.

I was just wondering if precise calculation of the angle is possible from geometry, but I could not workout how to do that.

 

[leo12345]

Thanks very much! In the attached PDF I found simple calculation. Distance of vanishing point from your eye sight point on the drawing is just a*tan(Theta) where a is the distance from your eye to the drawing and Theta is the angle of the wall with the the line from your eye to the drawing. This is a really good help for one who draws using perspective!

 

[Dr.Peterson]

Yes, it is possible; and you would do it by using math to determine where the vanishing points and the other points lie, and then finding angles from those precise coordinates on the drawing. The pages I referred to show at least some of that math (which is used, for example, in computer graphics), some of which may be over your head, but other parts may be not too bad.

Given coordinates of the points and lines in space, and of the plane of the drawing, you can find the locations of points on the drawing (exactly) where rays of light from the objects in the scene intersect the drawing plane. The principle is straightforward; carrying it out would take a lot of work. It will not be a single simple formula.