How far will my light reach

J

jasonmcbride

New member
Joined
Mar 9, 2020
Messages
10
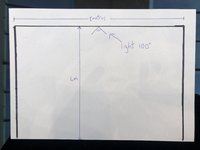
I want to buy lighting for my shed but not sure if I'll need 1 or 2. The shed is 8mx8m x 4m high and the light is 100 degrees angle. I have attached diagram.
I'm just not sure (and don't know how to work it out) if one light will reach the 8m width onto the floor 4m below.
Cheers
Jase
 

Attachments

  • IMG_5738.jpg
    IMG_5738.jpg
    1.7 MB · Views: 7
Make a drawing to scale, find a protractor or install an app, draw the angle, extend the lines to the floor.
 
jasonmcbride said:
Ok, thanks, is that the only way? not enough info to do it with maths?
Cheers
Jason
Click to expand...
Enough, but I thought you didn't need to be that precise.
How about this: draw the lines from from the center of the ceiling to the 2 bottom corners. What's the top angle of the triangle in the middle?
 
lev888 said:
Enough, but I thought you didn't need to be that precise.
How about this: draw the lines from from the center of the ceiling to the 2 bottom corners. What's the top angle of the triangle in the middle?
Click to expand...
I put it on the OP - 100 degrees
 
Don't forget (even if you use the scale drawing approach) that you presumably want to reach the corners of the floor, not just the middle of each side. You may want to draw a view along the diagonal from one corner to the opposite. How wide is that?

If you don't care about corners, then the answer to your question is very easy, almost obvious just from drawing what lev888 asked. If you do, then a little trig is needed.

(There's also the question whether the floor is all that has to be illuminated. Will you want to see anything on the walls, such as shelves?)
 
Dr.Peterson said:
Don't forget (even if you use the scale drawing approach) that you presumably want to reach the corners of the floor, not just the middle of each side. You may want to draw a view along the diagonal from one corner to the opposite. How wide is that?
Click to expand...
Good point, if the light source a regular bulb. If it's a long cylindrical fluorescent bulb type light then the difference between the middle and the corners will be pretty small.
 
Good point. We haven't been told a number of things, have we? If it is long, how long, and how does it shine off the ends? We were given 2-D information for a 3-D problem.

My image, when I think of a light bulb with a specified angle, is of a spot light or flood light's "beam angle", and that's also what I find when I search, e.g. here and here. Long bulbs/fixtures, in my (limited) experience, just shine everywhere; the closest I found was LED replacements for fluorescent bulbs, that can have a beam angle as small as 160 degrees -- no 100 degree angles.
 
If you'll want to use a workbench then you might want to have a light directly above that - or you could end up casting your own shadow onto everything that you try to do (if the only source of light is behind you)
 
Thanks everyone my trig understanding is very basic (I know Pythagoras ?)
The light I am buying is an led Highbay.
 
Last edited by a moderator:
Have you considered the questions we've discussed? Do you want the light to reach the corners of the floor, or any shelves or benches up on the walls?

Here's one way to answer your question:

Suppose you want the beam to reach a point on the floor [MATH]h[/MATH] meters down (4 in your example) and [MATH]d[/MATH] meters away from the point just below the light (4 if you want just to reach the base of the wall, half the width away, and half the diagonal if you want to reach the corners). Then we have a right triangle with angle [MATH]\theta[/MATH] equal to half the beam angle (50 degrees as stated, 57.5 degrees if the beam angle is 115 degrees as in your link). The adjacent leg is [MATH]h[/MATH], and the opposite leg is [MATH]d[/MATH]. So [MATH]\tan(\theta) = \frac{d}{h}[/MATH], and [MATH]\theta = \tan^{-1}(\frac{d}{h})[/MATH].

Do you know how to use the inverse tangent on a calculator?
 
You must log in or register to reply here.
Top