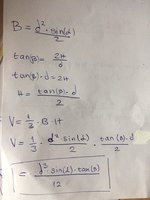How do I calculate the volume of a four-sided pyramid using only a diagonal and two angles?

[Ana.stasia]

The question is:
Calculate the volume of a four-sided pyramid If his base is a rectangle with a diagonal d, angle between two diagonals a (alpha) and an angle b (beta) between the edge of a pyramid and the base.

Basically I need to calculate the volume by only using d, a and b.

Here is how I tried to do it.



I tried to calculate the base, but I am not sure If this is correct and I don't know how to calculate the height of the pyramid. Also you see where I put a, the exact placement was not stated so would it make a difference if switched a and a1?

How can I calculate the volume?

Thank you in advance.

 

[Dr.Peterson]

If you moved your [MATH]\alpha[/MATH] to where [MATH]\alpha_1[/MATH] is that would only change the orientation of the rectangle. It makes no difference.

Your work for the area B is correct; to finish it, you might use the fact that [MATH]\sin(180^\circ - \alpha) = \sin(\alpha)[/MATH]. There are a couple ways you could have shortened the work, such as recognizing geometrically that [MATH]P_1 = P_2[/MATH].

As for finding H, how about using [MATH]\tan(\beta)[/MATH]?

Your thinking, on the whole, is very good.

 

[Ana.stasia]

If you moved your [MATH]\alpha[/MATH] to where [MATH]\alpha_1[/MATH] is that would only change the orientation of the rectangle. It makes no difference.

Your work for the area B is correct; to finish it, you might use the fact that [MATH]\sin(180^\circ - \alpha) = \sin(\alpha)[/MATH]. There are a couple ways you could have shortened the work, such as recognizing geometrically that [MATH]P_1 = P_2[/MATH].

As for finding H, how about using [MATH]\tan(\beta)[/MATH]?

Your thinking, on the whole, is very good.

Thank you. I managed to solve it.