How did I get a negative volume with Washer Method?

[Shutterbug424]

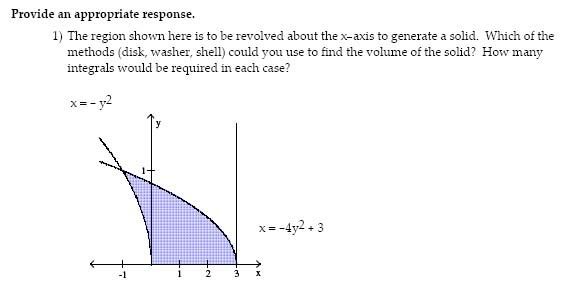
I got the volume using the shell method as being \(\displaystyle {\frac{{3\pi}}{{ 2}}}\)

When I used the washer method, I took 2 integrals.

This was the first one:
\(\displaystyle V = \pi \int\limits_{ - 1}^0 {\left( {\sqrt {\frac{{x - 3}}{{ - 4}}} } \right)} ^2 - \left( { \sqrt { - x}} \right)^2 dx\)

\(\displaystyle = \pi \int\limits_{ - 1}^0 {\frac{x}{{ - 4}}} + \frac{3}{4} + x dx\)

When I evaluate it, I get a negative answer which couldn't possibly be right. I noticed when I switch some of the positive and negative signs, I get the answer I need to get,
which is \(\displaystyle \frac{{3\pi }}{8}\)

The second equation I evaluated was:
\(\displaystyle V = \pi \int\limits_0^3 {\left( {\sqrt {\frac{{x - 3}}{{ - 4}}} } \right)} ^2 dx\)

I found this to be \(\displaystyle \frac{{9\pi }}{8}\)

When I add \(\displaystyle \frac{{3\pi }}{8}\) and \(\displaystyle \frac{{9\pi }}{8}\), I get \(\displaystyle \frac{{3\pi }}{2}\) (which I believe to be the correct answer).

My question is, where did I go wrong in the first equation that it didn't exactly work out to be \(\displaystyle \frac{{3\pi }}{8}\)?

 

[mmm4444bot]

... My question is, where did I go wrong in the first equation that it didn't exactly work out to be \(\displaystyle \frac{{3\pi }}{8}\)?

Hi Shutterbug:

It looks to me like you might have evaluated the integral incorrectly; I'm not sure because I'm not able to see how you arrived at -3?/8.

Both of your first two equations work out to V = 3?/8, for me.

Cheers,

~ Howard I. Noe

 

[Shutterbug424]

Thanks for your help

I evaluated yours, and I still got a negative 3pi/8

I must be doing something wrong. When I have a radical squared, does that just leave behind what was under the radical? Or does it somehow change signs?

 

[mmm4444bot]

... I must be doing something wrong ...

I think so. If you show your work, then you give us a chance to find any error(s).

... When I have a radical squared, does that just leave behind what was under the radical? YES

Or does it somehow change signs? NO

 

[Shutterbug424]

So, with your method

\(\displaystyle v = \frac{\pi }{4}\int\limits_{ - 1}^0 {\left( {\sqrt {3 - x} } \right)} ^2 dx - \pi \int\limits_{ - 1}^0 {\left( {\sqrt -x } \right)} ^2 dx\)

\(\displaystyle = \frac{\pi }{4}\int\limits_{ - 1}^0 {\left( {3 - x} \right)} dx - \pi \int\limits_{ - 1}^0 {\left( { - x} \right)} dx\)

\(\displaystyle = \frac{\pi }{4}\left[ {3x - \frac{{x^2 }}{2}} \right]_{ - 1}^0 - \pi \left[ {\frac{{ - x^2 }}{2}} \right]_{ - 1}^0\)

\(\displaystyle = \frac{\pi }{4}\left( { - 3 - \frac{1}{2}} \right) + \frac{\pi }{2}\)

\(\displaystyle = \frac{{ - 7\pi }}{8} + \frac{{4\pi }}{8} = \frac{{ - 3\pi }}{8}\)

 

[mmm4444bot]

...

\(\displaystyle = \frac{\pi }{4}\left[ {3x - \frac{{x^2 }}{2}} \right]_{ - 1}^0 - \pi \left[ {\frac{{ - x^2 }}{2}} \right]_{ - 1}^0\)

\(\displaystyle = \frac{\pi }{4}\left( { - 3 - \frac{1}{2}} \right) + \frac{\pi }{2}\)

It looks to me that you've evaluated these integrals by simply plugging in -1 into an antiderivative. That's not how we evaluate integrals.

We need to use BOTH of the endpoints of the interval when evaluating a definite integral.

EG:

\(\displaystyle \left. \frac{1}{x} \right|_{ a }^b \;=\; \frac{1}{b} \;-\; \frac{1}{a}\)

Does the following make sense?

\(\displaystyle = \frac{\pi }{4} \cdot \left( {0 - (-3) - (-\frac{1}{2})} \right) + \pi \cdot \left( 0 - \frac{1}{2} \right)\)

Your original method is also valid; perhaps, you made the same mistake evaluating that one.

~ Howard I. Noe

 

[Shutterbug424]

Yes. Thank you!

I guess I was just so used to rejecting zero because it is usually the lesser value. Thanks for curing my tunnel-vision

 

[mmm4444bot]

...Thanks for curing my tunnel-vision

I would like you to realize how much easier (for everyone involved) and more quickly this error could have been resolved had you simply posted your work at the very beginning.