Help with Probability of a series of 3d6 rolls

[CupcakeRogue]

> the problem is to calculate the probability of succeeding an Advanced Test
> a normal test is comprised of a roll of 3 six sided dice and a target number (TN)
Ex : the tn is 10 you roll 3d6 and get [4,3,6] for a total of 13 which passes the test by
Beating the tn.
> a test passes the tn if the sum of the 3d6 dices is greater or equal with the tn
> the order of the rolls are important as the last die is denoted the stunt die (SD)
>An Advanced test is comprised of 3,4 or 6 normal tests, separately from the TN the advanced test has also a threshold (TH).
> we are going to denote SUM_TH the sum of the SD of all rolls that pass the TN if this sum is greater or equal than the TH.
> X is the roll modifier wich is added to each normal test
> Y is the stunt modifier that is added to SUM_TH for each passed normal test
Ex: 3 tests, TN - 10, TH - 5, X - 2, Y - 1
You roll 3d6+2 three times
[1,2,1] + 2 = 6 fails
[3,4,2] + 2 = 11 passes
[6,4,2] + 2 = 14 passes

The SUM_TH = ( 2+1 ) + ( 2+ 1 ) = 6 this passes the Advanced test

What's the probability of succeeding the advanced test ?
How does the X and Y influence the test ?
How do I calculate this, so I can create a table for each 3,4 and 6 test types ?

> useful information

There are 216 possible rolls on 3d6

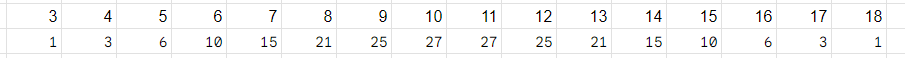
The sum on 3d6 varies on from 3 to 18 above is a table on how many of each sum are there (ex:
21 pair have the sum equal to 15)

> here is the probability for a roll to be equal to the TN and below the probability to be At least equal to the TN

 

[BigBeachBanana]

a normal test is comprised of a roll of 3 six sided dice and a target number (TN)

How are you determining the target number (TN)?

>An Advanced test is comprised of 3,4 or 6 normal tests, separately from the TN the advanced test has also a threshold (TH).

How are you determining the threshold?

> X is the roll modifier wich is added to each normal test
> Y is the stunt modifier that is added to SUM_TH for each passed normal test

How are you determining the X and Y

You roll 3d6+2 three times
[1,2,1] + 2 = 6 fails
[3,4,2] + 2 = 11 passes
[6,4,2] + 2 = 14 passes

The SUM_TH = ( 2+1 ) + ( 2+ 1 ) = 6 this passes the Advanced test

You said SUM_TH is the sum of the SD of all rolls that pass the TN and the modifier Y. In this case, shouldn't it be (2+2) + 1 = 5?
Where did the (2+1) + (2+1) come from?

 

[CupcakeRogue]

How are you determining the target number (TN)?


How are you determining the threshold?


How are you determining the X and Y


You said SUM_TH is the sum of the SD of all rolls that pass the TN and the modifier Y. In this case, shouldn't it be (2+2) + 1 = 5?
Where did the (2+1) + (2+1) come from?

The X,Y,TN,TH are given variables

In my example Y=1 and X=2
Y- is only added when calculating The SUM_TH
so it would be (2+Y)+(2+Y) = (2+1) + (2+1)

 

[blamocur]

What's the probability of succeeding the advanced test ?

What is the condition for the success of an advanced test?

 

[BigBeachBanana]

What is the condition for the success of an advanced test?

Based on the initial post, an advanced test can be type 3,4, or 6 meaning an advanced test type 3 comprises 3 normal tests and an advanced type 4 comprises 4 normal tests, and so on...

To pass the normal test, the sum of the dice roll plus X must be greater or equal to the target (TN)

To pass an advanced test, in each of the normal tests that are passed, sum up the last outcome of each normal test (stunt die) plus Y. If this sum is greater or equal to the threshold (TH), the advanced test is passed.