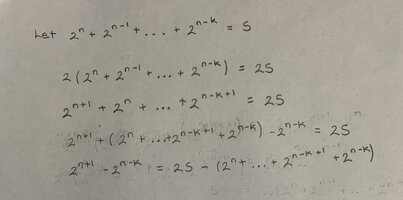Help Proving a Mathematical Identity

[DaRafster]

I'm instructed to prove the following identity:



However, I'm unsure how to prove this arithmetically.

I was given advice by my teacher to let the left hand side equal to S, then multiply both sides of the equation by two and distribute the two on the left hand side then go from there:



Ultimately, I was told that I should be able to get:

S = 2^(n+1) - 2^(n-k)

to which I've had no success in getting there so far.

What steps should I be taking to get to the desired answer?

I've attached a picture of my work below (you can see I'm just doing a bunch of arithmetic and getting nowhere):



This question has been gnawing at my head for the past hour and a half, making me question if it's even possible with this approach. I'm probably completely overlooking something or I'm doing something completely wrong which is why I've come to this forum to help me identify the issue.

 

[blamocur]

Does this help?:
[math]2^{n+1} + 2^n + 2^{n-1} + ... + 2^{n-k+1} =[/math][math]= 2^{n+1} + \left(2^n + 2^{n-1} + ... + 2^{n-k+1} + 2^{n-k}\right) - 2^{n-k}[/math]

 

[DaRafster]

Does this help?:
[math]2^{n+1} + 2^n + 2^{n-1} + ... + 2^{n-k+1} =[/math][math]= 2^{n+1} + \left(2^n + 2^{n-1} + ... + 2^{n-k+1} + 2^{n-k}\right) - 2^{n-k}[/math]

It did get me really close to the answer.

If I could get the right hand side to 2S - S, then I would arrive at my answer.

The problem is (2^n + ... + 2^(n-k+1) + 2^(n-k)) isn't exactly equal to S because of 2^(n-k+1).

There must be some small error I have or some additional step I could take to make this happen. However, I can't seem to figure out.

Here's my work and you'll understand what I'm saying.

 

[Harry_the_cat]

It did get me really close to the answer.

If I could get the right hand side to 2S - S, then I would arrive at my answer.

The problem is (2^n + ... + 2^(n-k+1) + 2^(n-k)) isn't exactly equal to S because of 2^(n-k+1).

There must be some small error I have or some additional step I could take to make this happen. However, I can't seem to figure out.

Here's my work and you'll understand what I'm saying.

Yes the bracket does equal S. The term 2^(n-k+1) is simply the term before 2^(n+k) in that sequence.

Note that the sequence is 2^n, 2^(n-1), 2^(n-2), up to 2^(n-k). Eg if k=7, the last term is 2^(n-7) and the second last term is 2^(n-6) ie 2^(n-7+1).

On your last line, replace the bracket with S because that is what S equals. Then what do you get?

 

[blamocur]

The problem is (2^n + ... + 2^(n-k+1) + 2^(n-k)) isn't exactly equal to S because of 2^(n-k+1).

Here is an equivalent notation but with [imath]2^{n-k+1}[/imath] hidden inside "..." :
[math]2^{n+1} + 2^n + 2^{n-1} + ... + 2^{n-k+1} =[/math][math]= 2^{n+1} + \left(2^n + 2^{n-1} + ... + 2^{n-k}\right) - 2^{n-k}[/math]

 

[DaRafster]

Yes the bracket does equal S. The term 2^(n-k+1) is simply the term before 2^(n+k) in that sequence.

Note that the sequence is 2^n, 2^(n-1), 2^(n-2), up to 2^(n-k). Eg if k=7, the last term is 2^(n-7) and the second last term is 2^(n-6) ie 2^(n-7+1).

Thank you! I failed to realize the terms in the brackets is actually equivalent to the sequence S. I was too fixed on having the terms inside the brackets look exactly like the one I had in the beginning.