HELP me SOLVE THE PROBLEM!

[carlycakes]

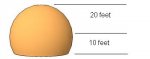
a dome is in the form of a partial sphere, with a hemisphere of a radius 20 ft on top and the remaining part of the sphere extending 10 feet to the ground from the center of the sphere. Find the surface area of the dome the the nearest square foot.
----------------
can you please show me step-by-step process to get the answer! thanksss!

 

[mmm4444bot]

the remaining part of the sphere extending 10 feet to the ground

I'm having trouble understanding your description of the dome.

Is the dome composed of a hemisphere on top of a cylinder, where both the hemisphere and cylinder have radius 20, and the cylinder has height 10 ?

OR, perhaps, the dome is a sphere, with the bottom vertical 10 feet missing, as in the image below.

Please clarify.

[attachment=0:14iof74l]MyOtherGuess.JPG[/attachment:14iof74l]

 

[carlycakes]

thats all the question...i wrote it exactly how it is

 

[galactus]

It would appear you are describing a 'zone' os the sphere as mmm has outlined. There is a portion of 10 feet under the ground, so to speak.

Use \(\displaystyle f(x)=\sqrt{20^{2}-x^{2}}, \;\ f'(x)=\frac{-x}{\sqrt{20^{2}-x^{2}}}\)

\(\displaystyle 1+[f'(x)]^{2}=\frac{400}{400-x^{2}}\)

\(\displaystyle S=2{\pi}\int_{-10}^{20}\sqrt{400-x^{2}}(\frac{20}{\sqrt{400-x^{2}}})dx\)

\(\displaystyle 2{\pi}\cdot 20\int_{-10}^{20}dx\)

This should give you the surface area of the exposed region.

We could also do this in general and show that the surface area depends only on the radius of the sphere and the height of the zone and not on the location of the zone.