carlycakes
New member
- Joined
- Aug 10, 2010
- Messages
- 8
Find the Volume of the solid generated by revolving the region about the y-axis.
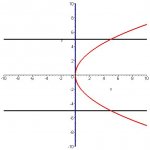
the region enclosed by x = y^2 / 5 , x = 0, y = -5, y = 5
can you please show me step-by-step process to get the answer! thanks!
the region enclosed by x = y^2 / 5 , x = 0, y = -5, y = 5
can you please show me step-by-step process to get the answer! thanks!