You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Hello, I'm stuck with an trig identity
- Thread starter saaz
- Start date
jonah2.0
Full Member
- Joined
- Apr 29, 2014
- Messages
- 544
Beer induced reaction follows.
 www.desmos.com
www.desmos.com
It's not an identity; you'll be stuck forever.Hello, I'm stuck with an trig identity, can someone help me? Thanks in advance ?
[math]-cot(x/2) = (sin2x+sinx)/(cos2x-cosx)[/math]
Saaz

saaz Hello, I'm stuck with an trig identity
jonah2.0
Full Member
- Joined
- Apr 29, 2014
- Messages
- 544
Beer induced reaction follows.
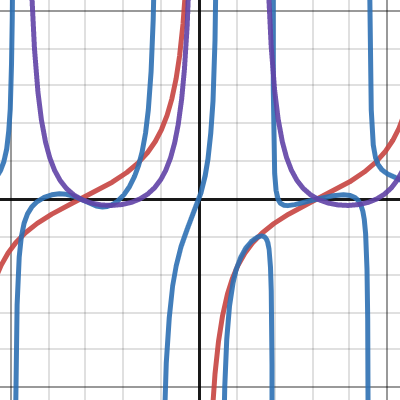
As you can see with the Desmos demigod, the red and blue graphs don't match.
Edit: Btw, what book wrere you using?
The Wolfram|Alpha god is clearly more hammered than I am.Really????????? Are sure? Fu**ing books that tell to verify each identity and don't say in the solutions that it is not. I've spent 4 hours on this thing. Jeez.
How did you get so quickly that it isn't an identity? Wolframalpha says this: View attachment 33520View attachment 33520
As you can see with the Desmos demigod, the red and blue graphs don't match.
Edit: Btw, what book wrere you using?
Last edited:
BigBeachBanana
Senior Member
- Joined
- Nov 19, 2021
- Messages
- 2,274
D
Deleted member 4993
Guest
sin(2x) + sin(x) = sin(3x/2 + x/2) + sin(3x/2 - x/2) = 2 * sin(3x/2) * cos(x/2)......editedHello, I'm stuck with an trig identity, can someone help me? Thanks in advance ?
[math]-cot(x/2) = (sin2x+sinx)/(cos2x-cosx)[/math]
Saaz
cos(2x) - cos(x) → -2 * sin(3x/2) * sin(x/2)
[sin(2x) + sin(x)] / [cos(2x) - cos(x)] = [2 * sin(3x/2) * cos(x/2)] / [-2 * sin(3x/2) * sin(x/2)] = - cot(x/2).......edited
Last edited by a moderator:
jonah2.0
Full Member
- Joined
- Apr 29, 2014
- Messages
- 544
Beer induced reaction follows.
My bad.
Drunk finger.
Aye.There's an extra x in your equation. The very last one on the bottom. The identity is in fact true.
View attachment 33522
My bad.
Drunk finger.
Harry_the_cat
Elite Member
- Joined
- Mar 16, 2016
- Messages
- 3,760
I'd start off by using the double angle formulae to rewrite sin(2x) and cos(2x) in terms of sin x and cos x.
Factorise and cancel.
Then use the double angle formulae again to write sin(x) and cos(x) in terms of sin(x/2) and cos(x/2).
Cancel and it all falls out.
Show us what you have done.
Factorise and cancel.
Then use the double angle formulae again to write sin(x) and cos(x) in terms of sin(x/2) and cos(x/2).
Cancel and it all falls out.
Show us what you have done.
Thank you all! I think I have to start again the chapter...
Meanwhile
Second, I don't see how this [2 * sin(3x/2) * sin(x/2)] / [-2 * sin(3x/2) * sin(x/2)] is equivalent to the - cot(x/2). I also checked in the graphic calculator, but it is not.
Anyway, now that I use the sum to product identity it's actually quite simple...

Meanwhile
Thanks! this is black magic. Can you tell me how did you get the last Sin(x/2) of the first line? Because from the double angle identity it comes out as a cos(x/2)...sin(2x) + sin(x) = sin(3x/2 + x/2) + sin(3x/2 - x/2) = 2 * sin(3x/2) * sin(x/2)
cos(2x) - cos(x) → -2 * sin(3x/2) * sin(x/2)
[sin(2x) + sin(x)] / [cos(2x) - cos(x)] = [2 * sin(3x/2) * sin(x/2)] / [-2 * sin(3x/2) * sin(x/2)] = - cot(x/2)
Second, I don't see how this [2 * sin(3x/2) * sin(x/2)] / [-2 * sin(3x/2) * sin(x/2)] is equivalent to the - cot(x/2). I also checked in the graphic calculator, but it is not.
Anyway, now that I use the sum to product identity it's actually quite simple...

I was using the double angle formulae, I factorised the nominator, but I didn't manage to find a way to factorise the denominator (after using the double angle identity to cos(2x).I'd start off by using the double angle formulae to rewrite sin(2x) and cos(2x) in terms of sin x and cos x.
Factorise and cancel.
Then use the double angle formulae again to write sin(x) and cos(x) in terms of sin(x/2) and cos(x/2).
Cancel and it all falls out.
Show us what you have done.
Last edited:
BigBeachBanana
Senior Member
- Joined
- Nov 19, 2021
- Messages
- 2,274
Perhaps you were seeing double, a common side effect of alcohol.Beer induced reaction follows.
Aye.
My bad.
Drunk finger.
Last edited:
Harry_the_cat
Elite Member
- Joined
- Mar 16, 2016
- Messages
- 3,760
\(\displaystyle cos(2x) - cos(x) = 2 cos^2(x) -1 - cos(x) =2cos^2(x) - cos(x) -1\)
Letting \(\displaystyle a=cos(x)\), you have \(\displaystyle 2a^2-a-1\). Can you factorise that?
Letting \(\displaystyle a=cos(x)\), you have \(\displaystyle 2a^2-a-1\). Can you factorise that?
Ooh, now I see: (2cos(x)+1)(cos(x)-1).\(\displaystyle cos(2x) - cos(x) = 2 cos^2(x) -1 - cos(x) =2cos^2(x) - cos(x) -1\)
Letting \(\displaystyle a=cos(x)\), you have \(\displaystyle 2a^2-a-1\). Can you factorise that?
Thanks again, you were super helpful.
jonah2.0
Full Member
- Joined
- Apr 29, 2014
- Messages
- 544
Beer soaked ramblings follow.
Me beer goggles can be very untrustworthy when I'm lying down on me bed with my phone clamped with one of them convenient phone holder thingamajigs. Good way to fall sleep while watching YouTube vids. Especially when I'm watching one them uploaded Ancient Aliens episodes; the narrator's voice really lulls me to sleep even without beer in me veins.
Definitely.Perhaps you were seeing double, a common side effect of alcohol.
Me beer goggles can be very untrustworthy when I'm lying down on me bed with my phone clamped with one of them convenient phone holder thingamajigs. Good way to fall sleep while watching YouTube vids. Especially when I'm watching one them uploaded Ancient Aliens episodes; the narrator's voice really lulls me to sleep even without beer in me veins.
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,561
After 4 hours (actually sooner) I would get suspicious that this was not an identity and plug in random values for x and see if both sides are equal. If they are not, then it is in fact not an identity and there is no need to continue. If on the other hand, you keep getting equality then you could assume that it is an identity and continue on.



