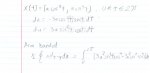You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Green's Theorem and a Hypocycloid
- Thread starter meks0899
- Start date
Looks like you're doing OK. But lets whittle it down a little more to something easier to deal with.
\(\displaystyle A=\frac{1}{2}\oint_{C} -ydx+xdy\)
\(\displaystyle =\frac{1}{2}\int_{0}^{2\pi}(3a^{2}sin^{4}(t)cos^{2}(t)+3a^{2}cos^{4}(t)sin^{2}(t))dt\)
\(\displaystyle =\frac{3}{2}a^{2}\int_{0}^{2\pi}sin^{2}(t)cos^{2}(t)dt\)
\(\displaystyle =\frac{3}{8}a^{2}\int_{0}^{2\pi}sin^{2}(2t)dt\)
Now, can you finish integrating that?.
\(\displaystyle A=\frac{1}{2}\oint_{C} -ydx+xdy\)
\(\displaystyle =\frac{1}{2}\int_{0}^{2\pi}(3a^{2}sin^{4}(t)cos^{2}(t)+3a^{2}cos^{4}(t)sin^{2}(t))dt\)
\(\displaystyle =\frac{3}{2}a^{2}\int_{0}^{2\pi}sin^{2}(t)cos^{2}(t)dt\)
\(\displaystyle =\frac{3}{8}a^{2}\int_{0}^{2\pi}sin^{2}(2t)dt\)
Now, can you finish integrating that?.
Did you graph this. It is called a "four-cusped" hypocycloid.
Just for fun, here is some info you or others may fnd interesting. I do.
A hypocycloid is drawn by taking a smaller circle and putting a point on its circumference. Then, take the circle and roll it on the inside of a larger circle. This will create a hypocycloid with three cusps.
You are probably too young to remember a Spirograph. This was a cool toy back in the day that allowed one to draw all sorts of shapes like this by putting smaller circles in larger ones and rolling them around. I used to have one when I was a kid. Wish I still had it. I would appreciate it more today.
It has equations \(\displaystyle x=(a-b)cos{\phi}+bcos\left(\frac{a-b}{b}{\phi}\right)\)
\(\displaystyle y=(a-b)sin{\phi}-b\left(\frac{a-b}{b}{\phi}\right)\)
To get your 4-cusped hypocycloid, we let \(\displaystyle b=\frac{a}{4}\) into the x and y above, we get
\(\displaystyle x=\frac{3}{4}a\cdot cos(t)+\frac{1}{4}a\cdot cos(3t), \;\ y=\frac{3}{4}a\cdot sin(t)-\frac{1}{4}a\cdot sin(3t)\)
But, \(\displaystyle cos(3t)=4cos^{3}(t)-3cos(t), \;\ sin(3t)=3sin(t)-4sin^{3}(t)\)
Thus, \(\displaystyle x=a\cdot cos^{3}(t), \;\ y=a\cdot sin^{3}(t)\)
We can represent this same curve, rectangularly, as
\(\displaystyle x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}\)
Just for fun, here is some info you or others may fnd interesting. I do.
A hypocycloid is drawn by taking a smaller circle and putting a point on its circumference. Then, take the circle and roll it on the inside of a larger circle. This will create a hypocycloid with three cusps.
You are probably too young to remember a Spirograph. This was a cool toy back in the day that allowed one to draw all sorts of shapes like this by putting smaller circles in larger ones and rolling them around. I used to have one when I was a kid. Wish I still had it. I would appreciate it more today.
It has equations \(\displaystyle x=(a-b)cos{\phi}+bcos\left(\frac{a-b}{b}{\phi}\right)\)
\(\displaystyle y=(a-b)sin{\phi}-b\left(\frac{a-b}{b}{\phi}\right)\)
To get your 4-cusped hypocycloid, we let \(\displaystyle b=\frac{a}{4}\) into the x and y above, we get
\(\displaystyle x=\frac{3}{4}a\cdot cos(t)+\frac{1}{4}a\cdot cos(3t), \;\ y=\frac{3}{4}a\cdot sin(t)-\frac{1}{4}a\cdot sin(3t)\)
But, \(\displaystyle cos(3t)=4cos^{3}(t)-3cos(t), \;\ sin(3t)=3sin(t)-4sin^{3}(t)\)
Thus, \(\displaystyle x=a\cdot cos^{3}(t), \;\ y=a\cdot sin^{3}(t)\)
We can represent this same curve, rectangularly, as
\(\displaystyle x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}\)
BigGlenntheHeavy
Senior Member
- Joined
- Mar 8, 2009
- Messages
- 1,577
\(\displaystyle Another \ Way.\)
\(\displaystyle Let \ y \ = \ g(t) \ = \ acos^{3}(t) \ and \ x \ = \ f(t) \ = \ asin^{3}(t), \ 0 \ \le \ t \ \le \ 2\pi.\)
\(\displaystyle Hence, \ \int_{a}^{b}ydx \ = \ \int_{t_1}^{t_2}g(t)f'(t)dt\)
\(\displaystyle Ergo, \ 4 \int_{0}^{\pi/2}acos^{3}(t)[3asin^{2}(t)cos(t)]dt \ = \ 12a^{2}\int_{0}^{\pi/2}cos^{4}(t)sin^{2}(t)dt\)
\(\displaystyle 12a^{2}\int_{0}^{\pi/2}cos^{4}(t)[1-cos^{2}(t)]dt \ = \ 12a^{2}\int_{0}^{\pi/2}cos^{4}(t)dt-12a^{2}\int_{0}^{\pi/2}cos^{6}(t)dt\)
\(\displaystyle =12a^{2}\bigg(\frac{3\pi}{16}\bigg)-12a^{2}\bigg(\frac{15\pi}{96}\bigg) \ (Wallis's \ Formulas) \ = \ \frac{3a^{2}\pi}{8}.\)
\(\displaystyle Let \ y \ = \ g(t) \ = \ acos^{3}(t) \ and \ x \ = \ f(t) \ = \ asin^{3}(t), \ 0 \ \le \ t \ \le \ 2\pi.\)
\(\displaystyle Hence, \ \int_{a}^{b}ydx \ = \ \int_{t_1}^{t_2}g(t)f'(t)dt\)
\(\displaystyle Ergo, \ 4 \int_{0}^{\pi/2}acos^{3}(t)[3asin^{2}(t)cos(t)]dt \ = \ 12a^{2}\int_{0}^{\pi/2}cos^{4}(t)sin^{2}(t)dt\)
\(\displaystyle 12a^{2}\int_{0}^{\pi/2}cos^{4}(t)[1-cos^{2}(t)]dt \ = \ 12a^{2}\int_{0}^{\pi/2}cos^{4}(t)dt-12a^{2}\int_{0}^{\pi/2}cos^{6}(t)dt\)
\(\displaystyle =12a^{2}\bigg(\frac{3\pi}{16}\bigg)-12a^{2}\bigg(\frac{15\pi}{96}\bigg) \ (Wallis's \ Formulas) \ = \ \frac{3a^{2}\pi}{8}.\)