Graphing (x+1)^3/(x-1)^2 controversial

[rexexdesign]

Hi everybody,

sorry to bother you on the weekend, but I am stuck on a problem that is giving me some trouble.
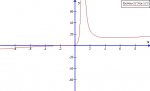
(x+1)^3/(x-1)^2

I have to find 1. & 2. derivative, domain, end behavior, extreme values, asymptotes, concavity and graph the function.

This is what I found so far: (correct me if I'm wrong)

domain: (-inf, 1) u (1, inf) *when I used online graphing calculator this function seems to be only (-inf, 1) but my reasoning says otherwise

symmetry: none

V.A. x=1

lim f(x) = inf
x->inf

lim f(x)=-inf
x->-inf

first derivative: [(x+1)^2(x-5)]/(x-1)^3

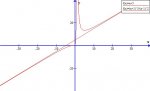
second derivative: having a real hard time figuring it out

critical points: x=-1, 5 f(-1)=0 local min f(5)=32 doesnt seem to be min or max

I got to the first line of the image below of the second derivative and online it says to simlify, but I dont see how they get the last step, can anybody help?

http://www.freemathhelp.com/forum/download/file.php?mode=view&id=104&sid=221c5b60278c135e29fa6246a1f6a409
simplify.jpg

can anybody post a screenshot of how the function is supposed to look, because I have the feeling that the free online java based graphing calculators are not getting it right.

 

[galactus]

The graph shows a vertical asymptote at x=1, which you can easily see. Therefore, the domain is everything but x=1.

There is no horizontal asymptote because the power of the numerator is greater than the power of the denominator.

But...here's the tricky part. It has an oblique asymptote at y=x+5

Upon long dividing we get \(\displaystyle \frac{4(3x-1)}{(x-1)^{2}}+\underbrace{x+5}_{\text{oblique asymptote}}\)

Plus, you can see it in the first graph I attached.

\(\displaystyle f'(x)=\frac{(x-5)(x+1)^{2}}{(x-1)^{3}}\)

\(\displaystyle f''(x)=\frac{24(x+1)}{(x-1)^{4}}\)

 

[rexexdesign]

Wow thanks sooo much for the graphs (which program do you use? I guess the slant asymptote makes sense. Thanks so much for the hint, I think I should be able to figure it out. Could you take a look at my edited post above how to get the second derivative from where I am stuck?

Thanks

 

[galactus]

That graph comes from a freeware download. Go to http://www.padowan.dk and downlaod the graphing utitlity. It's free and very nice. I use it all the time.


We can divide and rewrite the first derivative as \(\displaystyle 1-\frac{4(3x+1)}{(x-1)^{3}}\)

Now, the 1 is easy. It's derivative is 0. So, we work on the other part.

Quotient rule:

\(\displaystyle \frac{(x-1)^{3}(12)-4(3x+1)(3)(x-1)^{2}}{(x-1)^{6}}\)

\(\displaystyle \frac{12}{(x-1)^{3}}-\frac{12(3x+1)}{(x-1)^{4}}\)

Multiply top and bottom of left side by (x-1):

\(\displaystyle \frac{(x-1)}{(x-1)}\cdot\frac{12}{(x-1)^{3}}-\frac{12(3x+1)}{(x-1)^{4}}\)

This makes the denominators the same and we can wite as one fraction:

\(\displaystyle \frac{12(x-1)-12(3x+1)}{(x-1)^{4}}\)

\(\displaystyle =\frac{-24x-24}{(x-1)^{4}}=\frac{-24(x+1)}{(x-1)^{4}}\)

Remember the negative from the beginning. That makes it positive and we have:

\(\displaystyle \frac{24(x+1)}{(x-1)^{4}}\)