Graphing shape formed by x^2+(y-x^(2/3))^2=5 on TI-nspire

[andrew1]

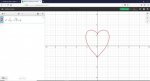
Hi there,
I am attempting to graph the shape of a heart on a TI-nspire cx cas calculator. The formula given is x^2+(y-x^(2/3))^2=5. This works perfectly well on desmos.com. I get an error on my calculator. The error is "relation input not supported." What can I do to graph it? I've found other formulas that do work, but I want to see if I can get this one to work as well.

For clarity, the equation is x squared plus open paren y minus x to the two thirds close paren squared equals five.

This is my first time posting; forgive me if the geometry section isn't the best place to be.
Andrew

 

[mmm4444bot]

The calculator may not be designed to plot implicit relationships.

Try solving the equation for y, first.

 

[mmm4444bot]

Solving the equation x^2 + (y - x^(2/3))^2 = 5 for y results in two solutions. One gives the upper portion (the other gives the lower portion) of the heart's right half.

Use what you know about reflecting graphs across the y-axis, to create the heart's left half. In other words, you need to plot four functions.

On this graph, I left a gap between the upper and lower portions.

 

[andrew1]

Thanks very much! I'm currently attempting to do that.

 

[andrew1]

I may have chosen a problem beyond me right now. I cannot get y on only one side of the equation, and am do not know how to find the two solutions for this type of problem. Do you have any hints on how I might do that?

I know what reflection is, but don't know how to write it in an equation.

 

[mmm4444bot]

I may have chosen a problem beyond me right now …

I can't tell. Are you taking a math class?

I solved the equation for y by (1) subtracting x^2 from each side, (2) taking the square root of each side, (3) considering both roots on the right and (4) adding x^(2/3) to each side.

When we take a square root while solving an equation, we almost always need to consider both (positive and negative) roots.

sqrt(u^2) = |u| = ±u

… I know what reflection is, but don't know how to write it in an equation.

Given f(x), we reflect across the vertical axis by plotting f(-x). That is, we change the sign on x, everywhere it appears in the definition for f(x).

If you would like more help, please show what you've done so far. Cheers :cool:

PS: Check out the forum guidelines; you can start with this summary.

 

[andrew1]

When we take a square root while solving an equation, we almost always need to consider the positive and negative root.

sqrt(u^2) = |u| = ±u

Given f(x), we reflect across the vertical axis by plotting f(-x). That is, we change the sign on x, everywhere it appears in the definition for f(x).

If you would like more help, please show what you've done so far. Cheers :cool:

PS: Check out the forum guidelines; you can start with this summary.

Hi again,
No, I'm not taking a math class. This all started when I couldn't figure out why my calculator wouldn't graph the original equation.
Thanks for your explanation about how you solved for y. I started by expanding (y-x^(2/3))^2 and was left with an algebraic mess of y=(5-x^2-x^4/3)/(y-2x^[2/3]). (Step by step at the bottom).

Can I ask for more explanation about "considering both roots?" There's a positive and negative sqrt(5), but I'm not sure how to complete your third step of "considering" them.
Would my two options be: y=-2.24-x+x^(2/3) and y=2.24-x+x^(2/3)? (Estimating the sqrt of 5). When I plug either of them into my graphing calculator, they go off into infinity, and don't end like I would want them to for the heart shape. They appear to be translated slightly by the change of sign in the sqrt(5) operation. How does that relate to the ultimate four functions I have to graph?

Failed attempt at solving for y:
Start with: x^2-(y-x^[2/3])=5
x^2+y^2-2yx^(2/3)+x^(4/3)=5
y^2-2yx^(2/3)=5-x^2-x^(4/3)
y(y-2x^[2/3])=5-x^2-x^(4/3)
y=(5-x^2-x^4/3)/(y-2x^[2/3])
Is any of the above remotely useful for my goal?

 

[mmm4444bot]

… No, I'm not taking a math class …

… Can I ask for more explanation about "considering both roots?" There's a positive and negative sqrt(5), but I'm not sure how to complete your third step of "considering" them …

I only meant: don't forget there's two square roots (the principal root and its opposite).

While solving an equation, many students will take the square-root of a symbolic square, such as \(\displaystyle \sqrt{u^2}\), and immediately write \(\displaystyle u\). In other words, they jump (from the square root of a symbolic square like \(\displaystyle u^2\)) to \(\displaystyle u\), without considering each root. They forget that:

\(\displaystyle \sqrt{u^2} \; = \; |u| \quad \text{not} \; u\)

… Would my two options be: y=-2.24-x+x^(2/3) and y=2.24-x+x^(2/3)? (Estimating the sqrt of 5).

No, those are not correct.

Also, you don't need to estimate √5 for your calculator.

Here are the steps that I suggested.


\(\displaystyle x^2 + (y - x^{2/3})^2 = 5\)


(1) \(\displaystyle \quad (y - x^{2/3})^2 = 5 - x^2\)

(2) \(\displaystyle \quad \sqrt{(y - x^{2/3})^2} = \sqrt{5 - x^2}\)

(3) \(\displaystyle \quad y - x^{2/3} = \pm\sqrt{5 - x^2}\)

(4) \(\displaystyle \quad y = \pm\sqrt{5 - x^2} + x^{2/3}\)


To get the left half of the plot, change x to -x. :cool:

 

[andrew1]

Thanks! I'm going to try finishing it. The last step leaves me with a thousand syntactical questions. I inverted the sign for both x but did not get what I was looking for. I'll keep trying...

 

[mmm4444bot]

… I inverted the sign for both x but did not get what I was looking for …

'Invert' is not the correct verb, here. You 'changed' the sign on x.

Make sure that you changed the sign and not the arithmetic operator.


EG: 10 - x^2

Change the sign on x

Correct: 10 - (-x)^2

Incorrect: 10 + x^2

 

[andrew1]

Ok, I've finally got it! Thanks again for your time. If you have a moment more, would you know where I could find more information about:
1. Why is there a gap in the heart in this equation, but not in the heart at Desmos.com, when we manipulated the same equation?
2. Where is there information about these types of formulas? I'd look it up myself, but I don't know the name of what I don't know about.
3. Is it possible to solve for y using the algebraic method I used? What I've found indicates the answer is no, but haven't found an absolutely sure answer, especially since I don't know much about what I want to look up.

You're the best!

Best,
Andrew

 

[andrew1]

'Invert' is not the correct verb, here. You 'changed' the sign on x.

Make sure that you changed the sign and not the arithmetic operator.


EG: 10 - x^2

Change the sign on x

Correct: 10 - (-x)^2

Incorrect: 10 + x^2

I used the "negative" sign as subtraction...rookie mistake.

 

[mmm4444bot]

… 1. Why is there a gap in the heart in this equation, but not in the heart at Desmos.com, when we manipulated the same equation?

The gap results from software differences. Look at the curve near the gap in post #3. Do you see how it's almost vertical, in that vicinity? In situations like this (where changes in x are much smaller than changes in y), the change in x might be smaller than what the software is designed to consider -- in some cases, the change in x might be less than one pixel's width. So, the software skips some points on the curve. Some graphers do a better job than others closing the gap because they're using finer increments in x to begin with or they have a setting to increase the number of sample points.

You can also try plotting over a shorter x interval (like -2.25 to 2.25); sometimes, that helps.

2. Where is there information about these types of formulas? …

Are you asking about equations (or sets of equations) whose graph forms a geometric shape? If so, I haven't seen a name for such a category.

There's a different coordinate system, where shapes are often seen. Google keywords polar equations and graphs. I'm guessing that you will need to change the graphing mode (to polar) on your calculator, to plot them.

3. Is it possible to solve for y using the algebraic method I used? …

No. When you expand \(\displaystyle (y - x^{2/3})^2\) it creates \(\displaystyle y^2\) and \(\displaystyle 2x^{2/3}y\) terms. Those are not like-terms in y; they cannot be combined into a single y-term. The only way to separate symbol y (after such an expansion) is to reverse the expansion and take square roots. :cool: