Graphing Extrema, Inflections, asymptotes

[SeekerOfDragons]

I'm having some issues in solving the following problem:

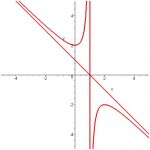
Graph the curve y = (-X^2 + 2X - 2) / (X - 1), showing all asymptotes, indicating any symmetries, indicate the intervals over which the graph is increasing, decreasing, concave up, concave down. Identify any relative extrema and points of inflection.

Asymptotes:
there is a vertical asymptote at X = 1. Found by setting (X - 1) = 0 X = 1
I have graphed the function on my calculator and know there is a diagonal down asymptote, but don't know how to calculate it.

To graph, I know you find the min/max by finding y' and solving for X and then plugging X into the original equation to get your points of min/max.

I have calculated y' to be (-X^2 + 2X) / (X - 1)^2
X = 0, X = 2.
Min/Max points are (0, 2) and (0, -2)

To find the points of inflection, you need to find y'', solve for X, plug that number in the original equation to get your points of inflection.

I have calculated y'' to be -2 / (X - 1)^3

If that's accurate, does that mean that there aren't any points of inflection?

If there are no points of inflection, then the function is decreasing (-infinity, 0) and (2, infinity) and increasing (0, 1) and (1, 2) Concave up (-Infinity, 1) and Concave down (1, infinity), Relative Min at (0, 2), Relative Max at (2, -2)

to summarize at this point I'm trying to figure out:

1. how do i calculate diagonal asymptotes.
2. am I correct in saying there are no points of inflection?
3. assuming no points of inflection, have I calculated the increasing, decreasing, concave up/down areas, relative min/max points correctly?

 

[chrisr]

You can write {-x[sup:2ida3ezo]2[/sup:2ida3ezo]+2x-2}/{x-1} as {-x[sup:2ida3ezo]2[/sup:2ida3ezo]+2x-1}/{x-1} - 1/{x-1}

which is (-x+1)(x-1)/(x-1) - 1/(x-1)

so the graph is also asymptotic to the line 1-x

 

[BigGlenntheHeavy]

\(\displaystyle f(x) \ = \ \frac{-x^{2}+2x-2}{x-1}\)

\(\displaystyle f'(x) \ = \ \frac{1}{(x-1)^{2}}-1, \ two \ critical \ points \ (0,2) \ and \ (2,-2)\)

\(\displaystyle f"(x) \ = \ \frac{-2}{(x-1)^{3}} \ = \ no \ points \ of \ inflection.\)

\(\displaystyle Vertical \ asymptote \ = \ x \ = \ 1, \ oblique \ asymptote \ = \ y \ = \ -x+1.\)

\(\displaystyle See \ graph.\)

[attachment=0:wbhokhwz]vwx.jpg[/attachment:wbhokhwz]

 

[SeekerOfDragons]

Ok, so I'm taking it then that I've correctly answered the question?

Vertical Asymptote: X = 1
Oblique Asymptote: 1 - X
Horizontal Asymptote: None

Symmetries: I can see a symmetry where X = 1 and y = 1 - X intersect... but how would I write that?

Graph is:
Increasing: (0, 1) and (1, 2)
Decreasing: (-infinity, 0) and (2, infinity)
Concave up: (-Infinity, 1)
Concave Down: (1, infinity)

Relative Max: (2, -2)
Relative Min: (0, 2)

Inflection: None

 

[chrisr]

Remember too that x=1 is not in the function domain,
so you can evaluate f(x) approaching +infinity and -infinity by examining f(x) to the immediate
left and right of f(x), which you appear to have done well.

How do you write the horizontal intervals if x=1 is not in the domain?
(0,1) or (0,1] ?

If you did not have the graph and you wanted to discover the second asymptote,
you can divide (x-1) into (-x[sup:15yaeovm]2[/sup:15yaeovm]+2x-2) which is 1-x remainder -1.
Hence we add 1 to the numerator and write

(-x[sup:15yaeovm]2[/sup:15yaeovm]+2x-2)/(x-1) is (-x[sup:15yaeovm]2[/sup:15yaeovm]+2x-1)/(x-1) - 1/(x-1)

This version has the left fraction evenly divisible by (x-1).

We get (-x+1)(x-1)/(x-1) - 1/(x-1).

As x approaches +infinity or -infinity, the term 1/(x-1) approaches zero, leaving (1-x),
hence the second asymptote is 1-x.

As x goes to + or -infinity, f(x) approaches the line 1-x.
As x goes to 1, f(x) goes to + or -infinity.