OK, I am having issues with a graphing calculator, because when I zoom out of the graph (containing exponents), the graph changes almost completely. If you could tell me which graph is right, or what is happening, and how to fix it if it isnt right.
The graphing calculator I am using is:
http://my.hrw.com/math06_07/nsmedia/tools/Graph_Calculator/graphCalc.html
The question I need to solve is:
I did the "Table of Values" for the function, but I need help on the graph.
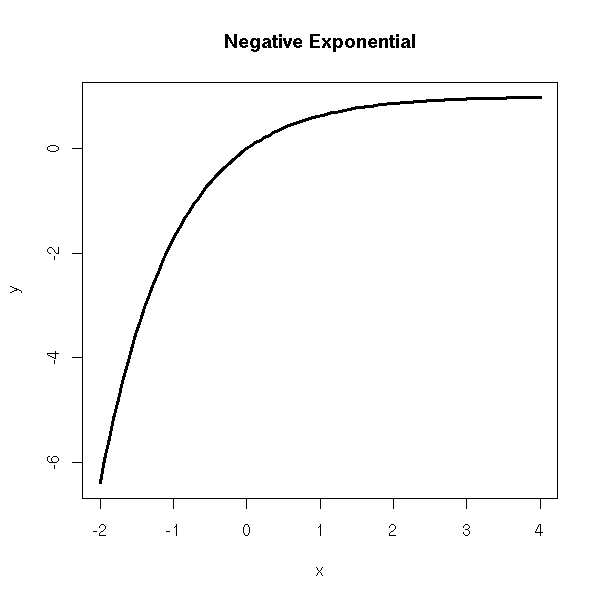
This is the the first graph:
y=(-2)?
x-min. = -10
x-max. = 10
x-scale = 1
y-min. = -10
y-max. = 10
y-scale = 1
http://img148.imageshack.us/img148/7930/pic2nb.png

This is the second graph zoomed out:
y=(-2)?
x-min. = -20
x-max. = 20
x-scale = 1
y-min. = -20
y-max. = 20
y-scale = 1
http://img444.imageshack.us/img444/3918/pic2n.png

And I dont know If this will help but this is an the "Table of Values" the graphing program gave me:
http://img245.imageshack.us/img245/4672/pic2d.png

So if anyone can help me out that would be great
Thanks,
Deo3560
The graphing calculator I am using is:
http://my.hrw.com/math06_07/nsmedia/tools/Graph_Calculator/graphCalc.html
The question I need to solve is:
Make your own table of values for the function y=(-2)?. Use the integers from -3 to +3 for your x values. Graph these points by hand on a sheet of paper. What happens to your graph?
I did the "Table of Values" for the function, but I need help on the graph.
This is the the first graph:
y=(-2)?
x-min. = -10
x-max. = 10
x-scale = 1
y-min. = -10
y-max. = 10
y-scale = 1
http://img148.imageshack.us/img148/7930/pic2nb.png

This is the second graph zoomed out:
y=(-2)?
x-min. = -20
x-max. = 20
x-scale = 1
y-min. = -20
y-max. = 20
y-scale = 1
http://img444.imageshack.us/img444/3918/pic2n.png

And I dont know If this will help but this is an the "Table of Values" the graphing program gave me:
http://img245.imageshack.us/img245/4672/pic2d.png

So if anyone can help me out that would be great
Thanks,
Deo3560