Graphing a simple summation to find area

[programmaChase]

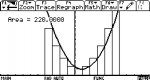
I'm not sure why I am having such trouble with this, but it has been boggling my mind for a couple hours now. How would I graph the limit of a summation in order to find the area under the curve 2x[sup:3efad7ua]2[/sup:3efad7ua] - 4x + 7 on the interval [-4,6] ? I've written the problem in sigma notation and solved it, yielding 275 sq. units, but looking back at my math I realize I have added 11 rectangles to obtain this answer when in fact in my graph of the summation I have only 10 rectangles to calculate the area under the curve (see below).

I know this is a very elementary question, but for whatever the reason I'm just not getting it. Thanks in advance for any help!

:rogrammaChase-::

 

[galactus]

What's wrong with your graph?. Here's a screen capture from my TI-92. I get 220 with it using 10 partitions and the right endpoint method. The actual integration value is \(\displaystyle \frac{650}{3}\)

 

[programmaChase]

Ok, I got 220 sq. units as you did -- my problem was that I was not remembering to use either right or left endpoint rule, therefore I was doing the following:

\(\displaystyle 1[f(-4) + f(-3) + f(-2) + f(-1) + f(0) + f(1) + f(2) + f(3) + f(4) + f(5) + f(6)]\)

which in turn caused me to sum 11 rectangles, instead of 10, giving me 275 sq. units. Everything makes sense now ! I appreciate the help and quick response!

:rogrammaChase-::