justan4cat
New member
- Joined
- May 23, 2010
- Messages
- 39
I think I have this one, but after the last question I posted, I'm not so sure. Can you please tell me if I'm correct? Here's the problem:
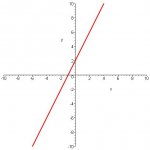
Graph the line for the equation: y+2=2(x+2)
First, I put it in linear equation form, y=mx+b and got y=2x+2
Then got the x and y intercepts:
y=0+2; y=2 so (0,2) is one point
0=2x+2; -2=2x; -1=x so (-1,0) is the other point and I just graph them.
The reason why I'm hesitating is because when I graph these two points and look at the slope, it is rise/run and that comes out to be 1/2, not 2.
Graph the line for the equation: y+2=2(x+2)
First, I put it in linear equation form, y=mx+b and got y=2x+2
Then got the x and y intercepts:
y=0+2; y=2 so (0,2) is one point
0=2x+2; -2=2x; -1=x so (-1,0) is the other point and I just graph them.
The reason why I'm hesitating is because when I graph these two points and look at the slope, it is rise/run and that comes out to be 1/2, not 2.