Graph Transformation Issue.

[Duston]

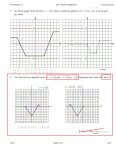
In the above question I'm asked to determine the difference between the 2 graphs one being "y=f(x)" the other being "y=f(a(x-b))". I am to find the values of "a and b." The graph has obviously flipped over the Y axis creating a Horizontal Invert but to create this you must have a "-" (negative) attached to the "x" value. Ie: y=f(a(-x-b)). If I attach a "-" (negative) to "a" it would flip the graph over the x axis creating a Vertical Invert. I don't understand how I can answer this question being able to only give the values of "a and b." I know I must be missing something here. please help.

 

[Ishuda]

Look at a corresponding line for each of the graphs: On the left hand side a line goes through (0, -6) and (4,1) giving line
L1: \(\displaystyle y\, =\, -6\, +\, \frac{7}{4}\, x\)
The corresponding line on the right goes through (-3,-6) and (-7,1) for
L2: \(\displaystyle y\, =\, -6\, -\, \frac{7}{4}\, (x\, +\, 3)\)

What would you have to substitute for x in L1 to get L2? What would you have to substitute for x in L2 to get L1?

 

[Duston]

Look at a corresponding line for each of the graphs: On the left hand side a line goes through (0, -6) and (4,1) giving line
L1: \(\displaystyle y\, =\, -6\, +\, \frac{7}{4}\, x\)
The corresponding line on the right goes through (-3,-6) and (-7,1) for
L2: \(\displaystyle y\, =\, -6\, -\, \frac{7}{4}\, (x\, +\, 3)\)

What would you have to substitute for x in L1 to get L2? What would you have to substitute for x in L2 to get L1?

I think I know what you're saying, but for this question I'm not suppose to be solving for X I'm only asked to determine the values of "a and b" within the given function. I'm learning transformations and transitions/reflections etc. (pretty new at this)

I am suppose to explain how Graph 1 has been transformed into Graph 2 by only selecting values for "a and b"

My issue is that I don't see how it's possible for Graph 1 to transform into Graph 2 without manipulating the "x" into a "-x." Given I'm not suppose to do that I'm uncertain how to answer this question.

 

[Ishuda]

I think I know what you're saying, but for this question I'm not suppose to be solving for X I'm only asked to determine the values of "a and b" within the given function. I'm learning transformations and transitions/reflections etc. (pretty new at this)

I am suppose to explain how Graph 1 has been transformed into Graph 2 by only selecting values for "a and b"

My issue is that I don't see how it's possible for Graph 1 to transform into Graph 2 without manipulating the "x" into a "-x." Given I'm not suppose to do that I'm uncertain how to answer this question.

Look at L1 and call it f(x),
f(x) = \(\displaystyle -6\, +\, \frac{7}{4}\, x\)
Now
f(a(x-b)) = \(\displaystyle -6\, +\, \frac{7}{4}\, a(x-b)\, = -6\, - \frac{7}{4} a\, b\, +\, a\, \frac{7}{4}\, x\)
for that to look like L2
L2: \(\displaystyle -6\, -\, \frac{7}{4}\, (x+3)\, = -6\, -\, 3\, *\, \frac{7}{4}\, -\, \frac{7}{4}\, x\)
what must the value of a and b be? So first translate the graph ? units right/left/up/down, then reflect/mirror/rotate/stretch/shrink the graph about the x/y axis or whatever.