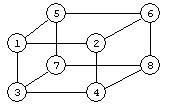
From what I know, the diameter of a graph is the distance between its furthest points.
The Girth of a graph is the shortest path from a vertex to itself.
Consider the following:
Define V to be the set of the 8 vertices of a cub. For any two elements p and q in V, and let {p,q} be an edge of G if and only if p and q belong to one and the same edge of the cube. Determine diameter and girth of G.
Im trying to draw this graph, but im a little confused as to what "if and only if p and q belong to one and the same edge of the cube" means.
I do know that it has 8 vertexs. But I don't know how to distingish which vertexs have a path.
The Girth of a graph is the shortest path from a vertex to itself.
Consider the following:
Define V to be the set of the 8 vertices of a cub. For any two elements p and q in V, and let {p,q} be an edge of G if and only if p and q belong to one and the same edge of the cube. Determine diameter and girth of G.
Im trying to draw this graph, but im a little confused as to what "if and only if p and q belong to one and the same edge of the cube" means.
I do know that it has 8 vertexs. But I don't know how to distingish which vertexs have a path.