Graph and best fit curve

M

Mira John

New member
Joined
Dec 8, 2020
Messages
4
Hello,
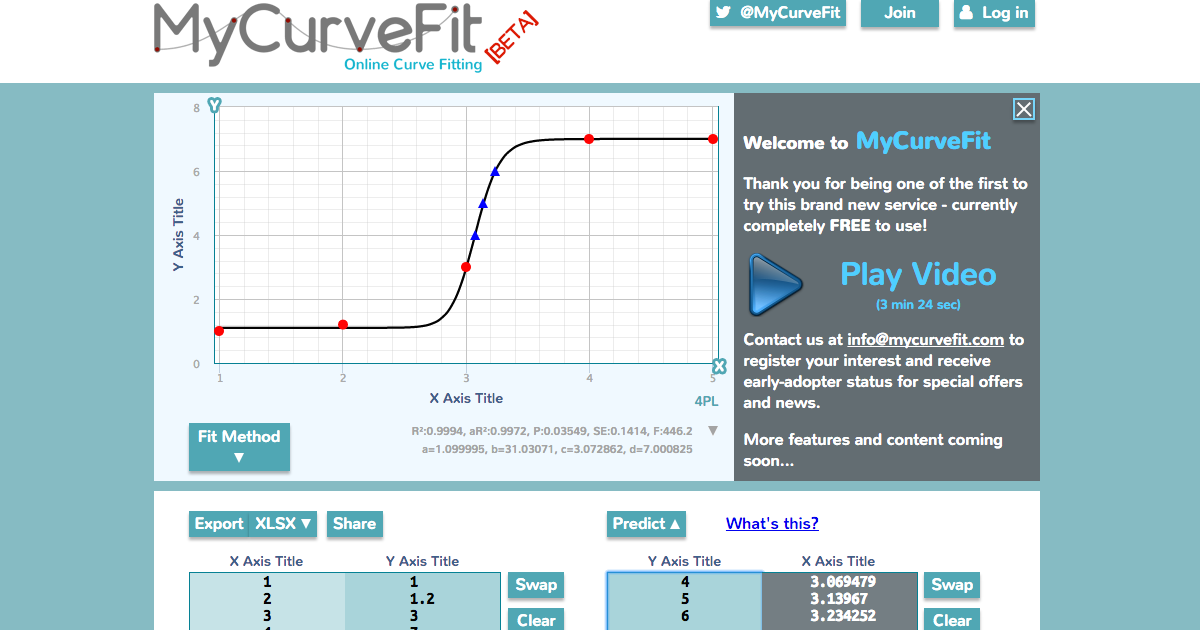
I would need help in fitting a curve to the following data, I have several curves and I need to find the equation of the best fit curve of each graph to combine them and find an overall equation. Excel best fit curves yield curves that are not close enough. Someone mentioned an exponential curve like 1-e^x but not sure this is a correct equation because it doesn't work with me, somehow looks like exponential but not sure of the correct equation. Would appreciate the help.
1607476953305.png
 
The best equation I can come up with is something like
[math]y = \dfrac{a}{x^2} ~ \left ( \dfrac{ e^{b/x} }{ e^{b/x} - 1 } \right ) + c[/math]
Here's an example. (Einstein's specific heat formula, second page at the top.)

Unfortunately I have no idea how to use this to fit a curve.

What are your choices?

-Dan
 
around x=5 it looks like the function would fail vertical line test, so you may have to use a spline
also how much accuracy do you need? cubic spline or bezier curve are the easiest. Bspline is more accurate but more work. If you don't need a lot of accuracy can't you just fit with a cubic or quartic polynomial using least squares? some other methods are lagrange interpolation or newton interpolation. They are all going to work. then you can convert to some kind of standard function
 
Last edited:
topsquark said:
The best equation I can come up with is something like
[math]y = \dfrac{a}{x^2} ~ \left ( \dfrac{ e^{b/x} }{ e^{b/x} - 1 } \right ) + c[/math]
Here's an example. (Einstein's specific heat formula, second page at the top.)

Unfortunately I have no idea how to use this to fit a curve.

What are your choices?

-Dan
Click to expand...

Thank you, I looked into it and it looks similar trend to my data, but not sure how to use it as well.
 
markraz said:
around x=5 it looks like the function would fail vertical line test, so you may have to use a spline
also how much accuracy do you need? cubic spline or bezier curve are the easiest. Bspline is more accurate but more work. If you don't need a lot of accuracy can't you just fit with a cubic or quartic polynomial using least squares? some other methods are lagrange interpolation or newton interpolation. They are all going to work. then you can convert to some kind of standard function
Click to expand...

Thank you for your reply, these are real data therefore some uncertainty is involved here. I need it to be very accurate because it will be used to get a correlation later. To be honest, I am not sure how to use what you have mentioned since I haven't dealt with them before, I used to use Excel to fit curves and it was working till I reached this type of trend which is not an easy Excel fit. I would appreciate any help or even a link to material that can help me understand it.
 
Mira John said:
Thank you for your reply, these are real data therefore some uncertainty is involved here. I need it to be very accurate because it will be used to get a correlation later. To be honest, I am not sure how to use what you have mentioned since I haven't dealt with them before, I used to use Excel to fit curves and it was working till I reached this type of trend which is not an easy Excel fit. I would appreciate any help or even a link to material that can help me understand it.
Click to expand...
All the standard fit methods I mentioned are equally as accurate in 2 dimensions. I would say the simplest 2D approach is to fit a polynomial using least squares regression. Looks like you only need a Quadratic or Cubic fit worst case. That is all excel is going to do. But excel is not very accurate. I think it's only accurate up to 8 decimal places on your input domain. The best thing to do is write a computer program using matrices. You can fit your curve using this standard formula:

(x,y) = ((A^T*A)^−1) * A^T * B

SOURCE : http://uregina.ca/~franklam/Math416/Math416_LeastSquares.pdf

some other links:
mathworld.wolfram.com

Least Squares Fitting--Polynomial -- from Wolfram MathWorld

Generalizing from a straight line (i.e., first degree polynomial) to a kth degree polynomial y=a_0+a_1x+...+a_kx^k, (1) the residual is given by R^2=sum_(i=1)^n[y_i-(a_0+a_1x_i+...+a_kx_i^k)]^2. (2) The partial derivatives (again dropping superscripts) are (partial(R^2))/(partiala_0) =...
mathworld.wolfram.com


some fit curve web sites where you can actually do it and get a polynomial:
great app here w/ source code:

not as good but still very good
mycurvefit.com

Online curve-fitting at mycurvefit.com

An online curve-fitting solution making it easy to quickly perform a curve fit using various fit methods, make predictions, export results to Excel,PDF,Word and PowerPoint, perform a custom fit through a user defined equation and share results online.
mycurvefit.com mycurvefit.com


You can also use Singular value decomposition to fit curves but it's more time consuming and really only worth the time if you are fitting planes:
 
Last edited:
oh by the way this x,y) = ((A^T*A)^−1) * A^T * B is called the
"The normal equation"
it's a very common formula used in many applications
mathworld.wolfram.com

Normal Equation -- from Wolfram MathWorld

Given a matrix equation Ax=b, the normal equation is that which minimizes the sum of the square differences between the left and right sides: A^(T)Ax=A^(T)b. It is called a normal equation because b-Ax is normal to the range of A. Here, A^(T)A is a normal matrix.
mathworld.wolfram.com
 
markraz said:
All the standard fit methods I mentioned are equally as accurate in 2 dimensions. I would say the simplest 2D approach is to fit a polynomial using least squares regression. Looks like you only need a Quadratic or Cubic fit worst case. That is all excel is going to do. But excel is not very accurate. I think it's only accurate up to 8 decimal places on your input domain. The best thing to do is write a computer program using matrices. You can fit your curve using this standard formula:

(x,y) = ((A^T*A)^−1) * A^T * B

SOURCE : http://uregina.ca/~franklam/Math416/Math416_LeastSquares.pdf

some other links:
mathworld.wolfram.com

Least Squares Fitting--Polynomial -- from Wolfram MathWorld

Generalizing from a straight line (i.e., first degree polynomial) to a kth degree polynomial y=a_0+a_1x+...+a_kx^k, (1) the residual is given by R^2=sum_(i=1)^n[y_i-(a_0+a_1x_i+...+a_kx_i^k)]^2. (2) The partial derivatives (again dropping superscripts) are (partial(R^2))/(partiala_0) =...
mathworld.wolfram.com


some fit curve web sites where you can actually do it and get a polynomial:
great app here w/ source code:

not as good but still very good
mycurvefit.com

Online curve-fitting at mycurvefit.com

An online curve-fitting solution making it easy to quickly perform a curve fit using various fit methods, make predictions, export results to Excel,PDF,Word and PowerPoint, perform a custom fit through a user defined equation and share results online.
mycurvefit.com mycurvefit.com


You can also use Singular value decomposition to fit curves but it's more time consuming and really only worth the time if you are fitting planes:
Click to expand...

Thank you so much @markraz, I appreciate all the info and the links you gave me, I will give it a try and read through the links you provided.
 
You must log in or register to reply here.
Top