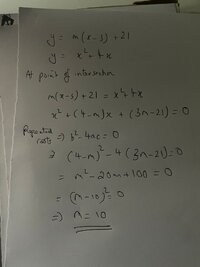Gradient at a point on a quadratic: gradient at (3, 21) for y = x^2 + 4x
- Thread starter apple2357
- Start date
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,619
The answer is correct; but it is possible to get a correct answer by a wrong method.
I'd say that this is "dodgy" in the sense that there is no explanation of why you can do what you are doing.
Can you explain why this should give the correct slope? What does each step mean?
I can't explain it. This is what i am really asking.
It started off as an attempt to use the intersection points of a general line that passes through the point with the given quadratic.
I actually wanted to form a quadratic in terms of x with 'm's and use the discriminant. But i didn't get that far and spotted this works but I don't understand why it works. It could be a fluke. If so tell me so!
The thing i am uncomfortable with is that i have cancelled an (x-3) but then substituted an x=3 to force the answer. It shouldn't work
It started off as an attempt to use the intersection points of a general line that passes through the point with the given quadratic.
I actually wanted to form a quadratic in terms of x with 'm's and use the discriminant. But i didn't get that far and spotted this works but I don't understand why it works. It could be a fluke. If so tell me so!
The thing i am uncomfortable with is that i have cancelled an (x-3) but then substituted an x=3 to force the answer. It shouldn't work
Last edited:
blamocur
Elite Member
- Joined
- Oct 30, 2021
- Messages
- 3,104
Trying to interpret a write-up which even its author does not understand would be a strange -- and not particularly useful -- exercise.
What have you learned? Do you know how to compute gradient, a.k.a. slope, of a function at a given point?
What have you learned? Do you know how to compute gradient, a.k.a. slope, of a function at a given point?
BigBeachBanana
Senior Member
- Joined
- Nov 19, 2021
- Messages
- 2,274
You're applying the definition of derivative.
[math]m =\lim_{x \to a} \dfrac{f(x)-f(a)}{x-a} =\lim_{x \to 3} \dfrac{(x^2+4)-21}{x-3} = \lim_{x \to 3}\dfrac{(x+7)(x-3)}{(x-3)}=\lim_{x \to 3 }x+7=10[/math]
That's why you're able to cancel out the [imath](x-3)[/imath]
That makes a lot of sense thank you. Its not what i was thinking but explains why the correct result stumbles out. Thank you again, you have changed my life!
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,561
(x-3)/(x-3) does NOT equal 1 when x=3! However, you want to what the slope approaches as x approaches 3. That is, x will be close to 3 but never 3 and in that case (x-3)/(x-3)=1.
Here is my advice. Never use a method that you don't understand as it is dangerous. Whatever you do you should have a reason why you think it is correct.
Here is my advice. Never use a method that you don't understand as it is dangerous. Whatever you do you should have a reason why you think it is correct.
The presentation is poor, (are we dividing both sides by zero on the last line ?), but looked at slightly differently the method is ok.
The parabola has the equation [imath]y=x^{2}+4x\dots(1),[/imath]
and the general equation of the straight line through the point (3, 21) is [imath]y=m(x-3)+21\dots(2),[/imath].
By solving the equations (1) and (2) simultaneously we're calculating the x coordinates of the points of intersection of the line and the parabola.
So, doing that, [math]x^{2}+4x=m(x-3)+21,\\ x^{2}+4x-21-m(x-3)=0,\\ (x-3) (x+7)-m(x-3)=0,\\ (x-3)(x+7-m)=0.[/math]So the line will intersect the parabola at x = 3 and x = m - 7.
If the line is to be a tangent to the curve the two roots must be equal, in which case 3 = m - 7, so m = 10, and the gradient of the line will then be equal to the gradient of the curve at that point.
The parabola has the equation [imath]y=x^{2}+4x\dots(1),[/imath]
and the general equation of the straight line through the point (3, 21) is [imath]y=m(x-3)+21\dots(2),[/imath].
By solving the equations (1) and (2) simultaneously we're calculating the x coordinates of the points of intersection of the line and the parabola.
So, doing that, [math]x^{2}+4x=m(x-3)+21,\\ x^{2}+4x-21-m(x-3)=0,\\ (x-3) (x+7)-m(x-3)=0,\\ (x-3)(x+7-m)=0.[/math]So the line will intersect the parabola at x = 3 and x = m - 7.
If the line is to be a tangent to the curve the two roots must be equal, in which case 3 = m - 7, so m = 10, and the gradient of the line will then be equal to the gradient of the curve at that point.
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,976
[imath]\lim_{x \to 3} \dfrac{(x^2+4)-21}{x-3} \large{\bf \ne} \lim_{x \to 3}\dfrac{(x+7)(x-3)}{(x-3)}[/imath] because [imath](x^2+4)-21\ne(x+7)(x-3)[/imath]
[imath][/imath][imath][/imath]
BigBeachBanana
Senior Member
- Joined
- Nov 19, 2021
- Messages
- 2,274
Yes, typo in post #8. Should be [imath]4x[/imath].Looks like [imath]4x[/imath] got replaced by plain [imath]4[/imath] at some point
Yes i had assumed every realised that was a typo, given the original problem!