Given Cot x = -5, sin x = sqrt(36)/26, evaluate 6 trig fcns

[NoAsherelol]

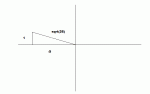
Given Cot x= -5 and sin x= (Sqaure root of 26)/26 evaluate all six trig functions

Im only in 10th grade why is this stuff so hard, i though trig functions are inbetween the intervals -1<0<1

 

[galactus]

Not all the trig functions are between -1 and 1 exclusively. csc, sec, cot have values > 1

Anyway, I posted a diagram to help get you started. See, by Pythagoras, we find that the hypoteneuse is

$\displaystyle r=\sqrt{(-5)^{2}+1^{2}}=\sqrt{26}$

Now, from that you can derive all the other ones.

We have $\displaystyle x=-5, \;\ y=1, \;\ r=\sqrt{26}$

You have sin(x), which is $\displaystyle \frac{y}{r}=\frac{1}{\sqrt{26}}=\frac{\sqrt{26}}{26}$

$\displaystyle \frac{x}{r}=cos(x)$

$\displaystyle \frac{y}{x}=tan(x)$

$\displaystyle \frac{r}{x}=sec(x)$

$\displaystyle \frac{r}{y}=csc(x)$

There, I am sure you can finish now. Okey-doke?.

 

[pka]

$\displaystyle \begin{array}{l} \sin (x) = \frac{{\sqrt {26} }}{{26}} = \frac{1}{{\sqrt {26} }}\,\& \,\cot (x) = - 5 \\ - 5 = \frac{{\cos (x)}}{{\sin (x)}} = \sqrt {26} \cos (x) \\ \end{array}$

 

[NoAsherelol]

yes i figured it out thanx for the help guys, i really appreciate it, i thought trig was fun lol, wish i was back in my 3rd grade days lol