Tsunamibomb
New member
- Joined
- Mar 21, 2023
- Messages
- 2
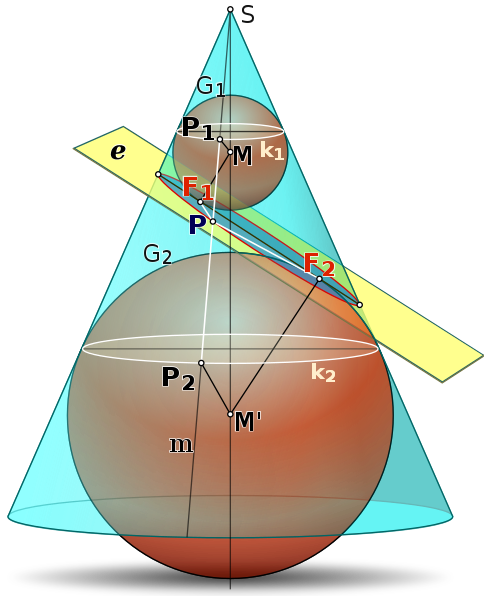
An ellipse is a conic section, i.e. it can be described as the surface of a cut through a cone. Given an ellipse, I want to calulate the properties of its corresponding cone and how it was cut out of it. I might later follow up with more questions about the relationship of an ellipse to a cone, but here we start:
- The end points of the major axis of the ellipse are points on the cone's surface (mantle) at different heights. What is the (circular) diameter of the cone at each of those two points?
- Given the proportions of the semi and major axes of the ellipse, what can be said about the apex angle of the cone, and the angle of the elliptic conic section plane to the cone's circular base plane?
Intuitively, I suppose that a combination of the cone's apex angle and the angle of the conic section cut to the base plane of the cone, might yield the same ellipse. If so, I'd like to know how the combination of those two properties of the cone can be restricted, given the properties of an ellipse.

- The end points of the major axis of the ellipse are points on the cone's surface (mantle) at different heights. What is the (circular) diameter of the cone at each of those two points?
- Given the proportions of the semi and major axes of the ellipse, what can be said about the apex angle of the cone, and the angle of the elliptic conic section plane to the cone's circular base plane?
Intuitively, I suppose that a combination of the cone's apex angle and the angle of the conic section cut to the base plane of the cone, might yield the same ellipse. If so, I'd like to know how the combination of those two properties of the cone can be restricted, given the properties of an ellipse.