Geometry

Should we assume that the angle will be the same regardless of relative sizes of the large and small squares?
 
Paul990 said:
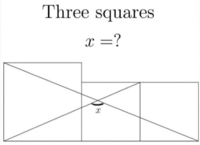
How do I find x
Click to expand...

It's right there in the middle ...


Evidently the idea is that you don't need to know the sides of the squares; if you trust that the problem has an answer at all, you could just pick a convenient size for the leftmost square and find the angle.

Or, you can call the side of the smaller squares 1, give a name to the side of the larger squares, and do some trigonometry.

I get the same answer by both methods. There may also be a direct geometrical approach, but I haven't tried yet.

Let's see your ideas.
 
Ha. Love your sense of humour! In the middle. Good one!
I'm thinking calling the side of the larger square 1. From there I'm seeing similar isosceles triangles. I know trig needs to be used somewhere, but where? I'm in the dark. Maybe the sine rule?
 
I myself used the right triangles HCJ and BHF to find the angles at H and C, and used those to find the angles at K:

1586525668161.png

Trying for a purely geometrical solution, I drew in some diagonals of squares and found some useful similar triangles, but couldn't prove all those that I needed.

I see no provably isosceles triangles as drawn. I'm not sure which triangles you have in mind. A couple look isosceles, but would not be if the larger square were a different size.
 
I tried looking at similar triangles. Using your drawings, triangle KJH and triangle KF-towards B, that intersects with KC. Then had a minor brain freeze and had to walk the dog to clear my head.
Then I came back and tried to superimpose the cartesian number plane and looked at point H as (0,0), point j as (0,1) and point C as (1+2x, 0) then point B as (1+x,0) and F as (1+x, x) then hit the wall.

And you were right, I though I was seeing isosceles triangles but i was wrong.
 
Did you try finding the tangents of angles FHC and JCH, in terms of x? Then use an angle-sum identity to find angle JKH, and hope that maybe x will cancel out ...

Coordinates can be another way toward the same idea.
 
It may be inapplicable for problem at this level, but I used vector-dot-product and got the angle to be 135o.

I took big square side to be 'a' and small square side to be 'b' - calculated unit vectors along CJ and HF - and used dot product (along with intrepid algebra).
 
Why would vectors be inapplicable? The problem doesn't say what level it is for.

But now that the answer is out there ...

My first method (at least to determine what the answer has to be if it exists) was to reduce the larger square to nothing, so my J and H are both at A, and see that FKC is obviously 45 degrees.

My full method was to take AB=BC=1 and HA=x, and to find that tan(FHC) = 1/(1+x) and tan(JCH) = x/(x+2). Putting these into the angle-sum formula for the tangent lead to tan(JKH) = 1.
 
Last edited:
I did a slightly different calculation as Dr. Peterson and agree with his result. But before I did that, I drew the thing out in Geogebra. Interestingly enough, Geogebra leads you to believe the angle is not constant as you vary the relative sizes of the squares. It gives the required angle at K as [MATH]135^\circ[/MATH] when the two small squares are the same size as the large one, with the angle increasing to about [MATH]155^\circ[/MATH] as you shrink the smaller squares. I think Geogebra is a great program, but I guess you need to be skeptical of its calculations.
 
I did the same. But my GeoGebra construction (see post #5) showed a constant 135 degrees. I wonder if yours was made incorrectly at some point. Make sure all your squares are really squares, for instance.

Now, I made the smaller squares fixed and varied the large one. That may be part of the difference in our constructions.
 
I used the regular 4 sided polygon for my squares and varied the size of the little ones. I had it calculate and show the measure of the angle. I didn't keep it but maybe I will redraw it and post it here if I can duplicate it again.
 
Too bad I didn't save it last night. But you are correct, I must have had something wrong. I just re-created it the same way (or so I thought) and it works like it should. Must have been a Gremlin...
 
You must log in or register to reply here.
Top