Taher has decided to create a triangular flower bed border. He plans to use 3 pieces of rectangular lumber with lengths 4, 5, and 6 feet, as shown in the figure below. Points A, B, and C are located at the corners of the flower bed.

1. Taher plans to cut the 3 pieces of lumber for the flower bed border from a single piece of lumber. Each cut takes
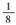 inch of wood off the length of the piece of lumber. Among the following lengths, in inches, of pieces of lumber, which is the shortest piece that he can use to cut the pieces for the flower bed border?
inch of wood off the length of the piece of lumber. Among the following lengths, in inches, of pieces of lumber, which is the shortest piece that he can use to cut the pieces for the flower bed border?
What's confusing: I don't even know how to start on this one. What do I even do with the info about the 1/8 piece of lumber?
2. After arranging the flower bed, Taher decides that the flower bed would look more attractive if 1 of the angles in the triangle were a right angle. He decides to place the right angle at vertex A and to leave the lengths of AB and AC as 4 and 5 feet, respectively. To the nearest 0.1 foot, how long of a piece of lumber would he need to replace the 6-foot piece represented by BC ?
What's confusing: Isn't A already a right angle?

1. Taher plans to cut the 3 pieces of lumber for the flower bed border from a single piece of lumber. Each cut takes
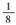
What's confusing: I don't even know how to start on this one. What do I even do with the info about the 1/8 piece of lumber?
2. After arranging the flower bed, Taher decides that the flower bed would look more attractive if 1 of the angles in the triangle were a right angle. He decides to place the right angle at vertex A and to leave the lengths of AB and AC as 4 and 5 feet, respectively. To the nearest 0.1 foot, how long of a piece of lumber would he need to replace the 6-foot piece represented by BC ?
What's confusing: Isn't A already a right angle?
Last edited:
